Viteza și accelerația drept coordonate derivate
mișcarea corpului se numește o schimbare a poziției sale în spațiu în raport cu celălalt.
Coordonarea - valoarea care servește pentru a determina poziția oricărui punct de pe plan sau în spațiu.

mișcarea corpului este vectorul care face legătura între poziția de pornire a corpului cu poziția sa ulterioară.
Traiectoria - o linie de-a lungul căreia corpul se mișcă.
Cale - o lungime de cale de-a lungul care corpul se mișcă.
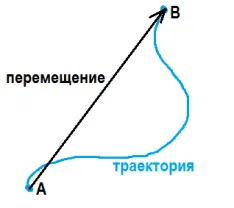
mișcare uniformă rectilinie se numește o mișcare în care corpul de orice intervale regulate, face aceeași mișcare.
Uniformă a vitezei de mișcare rectilinie este o cantitate egală cu deplasarea relativă a timpului t al corpului. pentru care a avut loc această mișcare.
viteză # 8213; este o cantitate vector!
Sarcinile, care arată dependența de viteza corpului din timp în timp.
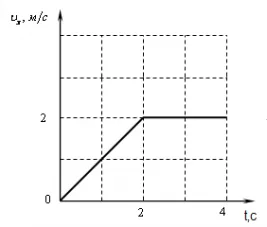
Distanța parcursă poate fi calculată ca aria de sub grafic.
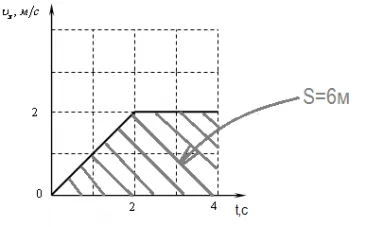
accelerare a corpului este o cantitate vector egal cu raportul dintre viteza de schimbare pentru orice perioadă de timp pentru amploarea acestui decalaj.
Timpul de dependență a vitezei în prezența accelerației dat de expresia. în cazul în care:
# 8213; viteza de corp la momentul t;
# 8213; viteza inițială a corpului;
# 8213; accelerare a corpului.
mișcare accelerată Uniform a corpului se numește o mișcare în care accelerarea acesteia nu se schimba, fie în mărime sau direcție.
Ecuația de mișcare uniform accelerată în proiecția pe axa x are forma:
x (t) = x 0 + v 0t +.
Unde x 0 # 8213; să coordoneze corpul inițial;
v 0 # 8213; proiecția vitezei inițiale la axa x;
o # 8213; proiecția accelerației pe axa x;
T # 8213; în timp ce conduceți.
Viteza și accelerația drept coordonate derivate
Dacă există o dependență de coordonatele x (t) de timp, dependența vitezei în funcție de timp poate fi obținută luând derivata de această dependență. viteză # 8213; un derivat al corpului de coordonate timp vx (t) = x „(t). De exemplu, în cazul în care coordonatele corpului cu dependență de mișcare uniform accelerată este de forma x (t) = 6 - 2t + 12T 2, luând apoi primul derivat al dependenței coordonate obținem viteza corpului de la vremenivx (t) = -2 + 12 # 8729; 2t = -2 + 24t.
În mod similar, accelerarea # 8213; Este un derivat al vitezei corpului. ax (t) = vx „(t).
Mișcarea circumferențial
Atunci când conduceți într-un cerc este adesea convenabil de a folosi nu viteza obișnuită, auglovuyu de viteză.
viteza unghiulară este numeric egală cu intervalul unghiului de rotire pe unitatea de timp.
Viteza unghiulară a corpului, se deplasează de la punctul 1 la punctul 2, va fi egal cu:
# 8710; # 966; # 8213; unghiul de rotație [rad]
# 8710; t # 8213; intervalul de timp [s],
# 969; # 8213; viteza unghiulară.
Viteza liniară a punctului la o anumită distanță (raza) R de axa de rotație poate fi considerată ca: v = # 969; R.
Prin urmare, mai mare raza cercului, cu atât mai mare viteza liniară, cu o viteză unghiulară constantă.

Perioada - timpul în care organismul face o rotație completă în jurul circumferinței.
R # 8213; raza cercului [m]
v # 8213; viteză.
Frecventa - egal cu numărul de spire dintr-un cerc realizat de o unitate de timp.
N # 8213; numărul de rotații.
Atunci când conduceți într-un cerc a corpului, în orice moment dat, își schimbă direcția vitezei sale și, prin urmare, se mișcă cu accelerație.
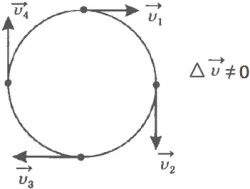
Accelerația experimentat de un corp în mișcare într-un cerc, numit normal sau centripetă și întotdeauna spre centrul cercului.
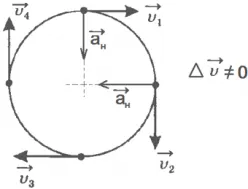
accelerație normală caracterizează viteza de schimbare în direcția și notată cu litera:
R # 8213; raza cercului [m]
o # 8213; accelerație normală,
v # 8213; viteză.