suspensie Trifilyarny
DEFINIREA MOMENTUL inerției ORGANISMELOR
PRIN TRIFILYARNOGO SUSPENDAREA
Scopul lucrării. determinarea momentului de inerție al unor organe în raport cu axa de rotație care trece prin centrul de masă, studiul privind influența momentului de inerție al axelor de rotație a transferului (teorema lui Steiner verificarea metoda vibrațiilor de torsiune).
Accesorii. suspensie trifilyarny, un cronometru, un corp șubler pentru măsurarea momentului de inerție.
Întrebările care sunt necesare pentru admiterea la executarea de lucrări
deplasare unghiulară. Unități de măsură.
Viteza unghiulară. Legătura dintre viteza de colț a corpului și viteza liniară a punctelor sale. Unități de măsură.
accelerația angulară. Legătura dintre accelerația unghiulară a corpului și accelerația liniară a punctelor sale. Unități de măsură.
Ceea ce se numește momentul de inerție al punctului material? Unități de măsură.
Ceea ce se numește momentul de inerție al corpului? Unități de măsură. Ce determină valoarea momentului de inerție?
Ce determină valoarea momentului de inerție?
Ceea ce se numește puterea umăr?
Ceea ce se numește momentul de forță? Unități de măsură.
Scrie și să explice ecuația fundamentală a dinamicii mișcării de rotație. Care este rolul momentului de inerție în această ecuație?
Formulați teorema lui Steiner.
Ce este trifilyarny suspensie?
De ce tensiunea trifilyarnogo fire de suspensie ar trebui să fie la fel?
Atunci când se analizează rotația corpului rigid cu punctul de vedere dinamic conceptul forțelor se înlocuiește cu conceptul de momentele forțelor, conceptul de masa - conceptul momentului de inerție. Dacă împărțiți rotativ mental corp solid în n elementar massDmi. la ri distanță de axa de rotație, atunci ei vor trebui să prezinte aceeași viteză unghiulară


Momentul de inerție Ji a punctului material este numeric egal cu produsul punctului de masă pe Dmi pătrat ri distanță de axa de rotație:
Momentul de inerție J a întregului corp al solidului este numeric egală cu suma tuturor momentelor de inerție ale punctelor sale:
Amploarea momentului de inerție depinde de distribuirea în masă a caracterului în raport cu axa de rotație și, prin urmare, același organism poate avea diferite momente de inerție axe diferite.
În cazul în care organismul se poate roti în jurul unei axe fixe, schimbarea în mișcarea ei depinde care acționează în momentul său de forță. Momentul unei forțe în jurul unei axe fixe este cantitatea care este numeric egal cu produsul dintre forța F pe ea umăr h. puterea Umăr - este cea mai mică distanță de centrul de rotație la linia de forță.
Mișcarea de rotație a corpului este caracterizat prin viteza unghiulară și unghiulare accelerație :
în cazul în care - mișcarea unghiulară a corpului.
Legea fundamentală a dinamicii mișcării de rotație, care exprimă dependența accelerației unghiulare a momentului a forței poate fi scrisă ca:
Din momentul de inerție depinde de masa distanței în raport cu axa
rotație, axa de deplasare atunci când momentul de inerție este schimbat. Momentul de inerție față de o axă care trece prin centrul de masă (J0), în majoritatea cazurilor, nu este greu de definit. În acest caz, cunoscând momentul de inerție față de axa de rotație care trece prin centrul de masă, este posibil de a găsi un moment în jurul oricărei axe paralelă cu prima.
Pentru cazul axelor paralele Teorema lui Steiner se aplică: momentul de inerție în jurul oricărei axe de rotație este egal cu suma momentului de inerție față de axa de rotație care trece prin centrul de masă, iar greutatea produsului pe pătratul distanței dintre axele (d):
De exemplu. Cploshnogo calcula momentul de inerție al tijei în raport cu axa lungimii l O'O'1. trecând prin capătul arborelui (Fig.1). Teorema Steiner J = J0 + md 2. Momentul de inerție în jurul axei oo1. care trece prin centrul de masă, J0 este egal cu:
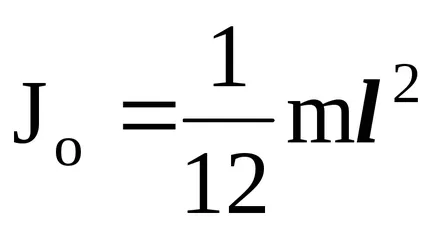
.
În practică, momentul de inerție poate fi determinată prin trifilyarnogo suspensie.
Trifilyarny suspensie este o platformă circulară suspendată pe trei fire plasate simetric, întărit la marginile platformei. Deasupra acestor fire sunt de asemenea simetric atașate la discul de diametru ceva mai mic decât diametrul platformei (fig. 2).
latforma poate efectua oscilații de torsiune în jurul unei axe verticale perpendiculare pe planul său și care trece prin centrul său. Centrul de greutate cu platforma se deplasează de-a lungul axei de rotație. Perioada de oscilație este determinată de momentul de inerție al platformei, acesta va fi diferit în cazul în care o platformă pentru a încărca orice alt organism. Acestea și se bucură în această lucrare. Momentul de inerție în această lucrare va fi calculată cu următoarea formulă.
Conform formulei (6) poate fi definit nu numai momentul de inerție al platformei, dar, de asemenea, corpul plasat pe ea, ca toate cantitățile de pe partea dreaptă a formulei poate fi măsurată direct.
Impulsul de rotație necesar pentru a începe oscilațiilor torsionale, potrivit unei platforme de discul de sus se rotește în jurul axei sale, prin intermediul unui cordon de tensiune, rezultând în mișcarea pârghiei asociate cu unitatea. Aceasta realizează o absență aproape completă a altor oscilații non torsionale a căror prezență complică măsurătoarea.
Ordinea executării
1. Inform platforma gol și puls rotativ este măsurat cu un cronometru în timp ce 20 de oscilații complete (t0), care permite să se determine cu precizie suficient de valoarea T0 perioadei.
2. Conform formulei (6) determină momentul de inerție J0 platformă goală.
3. Prin cântărirea greutatea determinată de test (m), și apoi încărcați-le pe platformă și din nou se măsoară timpul t 20 oscilație și apoi perioada de oscilație T a întregului sistem.
4. Conform formulei (6) calcularea momentului de inerție J1 întregului sistem. Luând greutatea sa egală cu cantitatea de greutate corporală (m) și platforma (m0). Amploarea momentului de inerție J este definită ca diferența dintre J = J1 - J0.
5. Datele înregistrate în tabelul 2 sunt calculate și erorile absolute și relative.
6. Suspensie Utilizați trifilyarnogo verificat Steiner teoremă. De ce este necesar să existe două corpuri complet identice.
În primul rând, se determină momentul de inerție al acestor organisme, punându-le una peste alta, în centrul platformei. Se măsoară timpul t 20 oscilație și apoi calculul perioadei de oscilație T a întregului sistem. Conform formulei (6) calcularea momentului de inerție J2 întregului sistem. Luând greutatea sa egală cu suma maselor (2m) și o platformă (m0). Amploarea momentului de inerție J2 „este definită ca diferența J2“ = (J2 - J0) / 2.
Apoi, cele două organisme sunt dispuse simetric pe platformă și să definească momentul lor de inerție. Se măsoară timpul t 20 oscilație și apoi calculul perioadei de oscilație T a întregului sistem. Conform formulei (6) calcularea momentului de inerție J3 întregului sistem. Luând greutatea sa egală cu suma maselor (2m) și o platformă (m0). Amploarea momentului de inerție J3 „este definită ca diferența J3“ = (J3 - J0) / 2. J3 „- momentul de inerție al corpului, situat la o distanță fixă față de axa de rotație.
Cunoscând această distanță, în greutate, moment de inerție, poziția în centrul platformei, este posibil să se verifice teorema lui Steiner.
7. Datele înregistrate în tabelul 3 sunt calculate și erorile absolute și relative.
8. Asigurați-masa. 1 trifilyarnogo parametrilor de măsurare a suspensiei și greutatea corporală.
1. Savelyev IV Curs de fizica generala. T. I. - M. Nauka, 1989.
2. Arhanghelul MM Cursul fizicii: mecanica. - M. Educație, 1975: I69-I93.
3. Liventsev NM fizica, M. curs Graduate School, 1974. § 11-13.
4. Grabowski VI fizica, M. curs Graduate School, 1970. §21-23.
5. P. Atkins Physical Chemistry. - Mir. 1980.
6. Katz TS.B. Biofizică la lecții de fizică. - M. Educație 1988.
Pentru credit este necesară
1. Să demonstreze profesorul capacitatea de a determina momentul de inerție prin trifilyarnogo suspensie.
2. Trimiterea un raport în forma prescrisă.
Pentru a fi în măsură să răspundă la întrebări, cum ar fi:
a) Poate fi considerată greutatea ca concentrată în centrul său, dacă doriți să calculeze momentul de inerție al corpului?
b) două din aceeași greutate și grosimea discului sunt fabricate din metale diferite densități. Care dintre ele are un moment mare de inerție?
c) este necesară pentru a determina momentul de inerție de forme geometrice complexe ale corpului. calcul matematic devine dificil. Se specifică metoda prin care momentul de inerție al corpului poate fi determinată experimental.
) In Fig. 4 este un corp a cărui axă de rotație trece prin punctul O, care este perpendicular pe desen. Cum de a determina momentul forței F, aplicată la punctul A (B)? Ca vector forță de cuplu vector direcționat al momentului unghiular?
d) Două cilindru solid, realizate din materiale diferite, au aceleași raze de masă și de bază. Comparați momentele lor de inerție despre tine-axe de simetrie.
e) Doi cilindri au aceeași dimensiune și greutate. Cum, folosind un plan înclinat, pentru a determina care dintr-un cilindru solid, un gol?
g) În ceea ce privește oricare dintre cele două axe de inerție mai mare, în raport cu axa care trece prin centrul de masă, sau în jurul unei axe care nu trece prin centrul de masă?
momente de inerție de masă