Sumar calcularea coordonatelor centrului de greutate a unei figuri plane

1. centrul de greutate coordonate.

Lăsați un sistem de puncte materiale de avion Oxy dat

P 1 (x 1, y 1); P 2 (x 2, y 2);. P n (x n, y n)

masele c m 1 m 2, m n m 3 ..

Compoziții x i m i și y i m i sunt numite momente statice in raport cu masa m i și Oy axele Ox.

Vom nota prin coordonatele x y c c și a centrului de greutate al sistemului. Apoi coordonatele centrului de greutate al sistemului materialului descris definit prin formulele:

Aceste formule sunt utilizate în determinarea centrelor de greutate ale diferitelor forme și organisme.

1. Centrul de greutate al unui plan figura.

Fie ca această cifră delimitată de liniile y = f 1 (x), y = f 2 (x), x = a, x = b, este o bucată de material plat. Densitatea de suprafață, respectiv masa pe unitatea de suprafață, presupusă a fi constantă și egală cu Ö pentru toate părțile din figură.

Împărțim această cifră drept x = a, x = x 1 x = x n = b în benzi de lățime de 1 x rmn, δ x δ x 2. n. Masa fiecărei benzi este egală cu produsul din suprafața acestuia la o densitate δ. Dacă fiecare bandă înlocuiți dreptunghi (figura 1), cu o bază δ x i și înălțimea f 2 (ξ) -f 1 (ξ), unde ξ. banda va fi aproximativ egală cu masa

Aproximativ centrul de greutate al benzii va fi în centrul dreptunghiului corespunzător:

Acum, înlocuind fiecare punct fâșie de material, masa, care este egală cu masa benzii respective și este concentrată în centrul de greutate al benzii, găsim o valoare aproximativă a centrului de greutate al întregii figură:

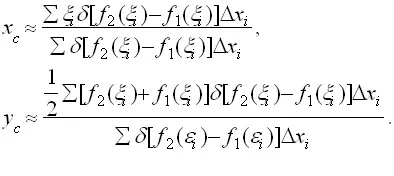
Trecerea la limita. Primim coordonatele exacte ale centrului de greutate al figurii:

Aceste formule sunt valabile pentru orice omogene (adică având o densitate constantă în toate punctele) planul fig. După cum se vede, poziția centrului de greutate nu depinde de cifra δ densitate (în procesul de calcul δ a scăzut).

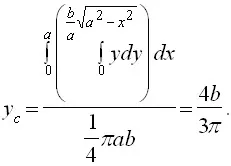
Găsiți coordonatele centrului de greutate al catenarei arcului.

1Tak curba este simetrică față de axa Oy, centrul de greutate se află pe axa Oy, și anume X c = 0. Rămâne de găsit. Apoi, avem lungimea arcului

Folosind Teorema Goulden găsi coordonatele centrului de greutate al unui cadran

.

La rotirea plăcii sfert cercul din jurul axei Ox obținem emisferei, al cărui volum este egal cu

Conform celei de a doua teoremă Goulden, aici un centru cadranului de greutate se află pe axa de simetrie, adică, Eu pe bisectoarea unghiului de coordonate, și, prin urmare,