Funcția de distribuție cumulativă normală - Enciclopedia economiei
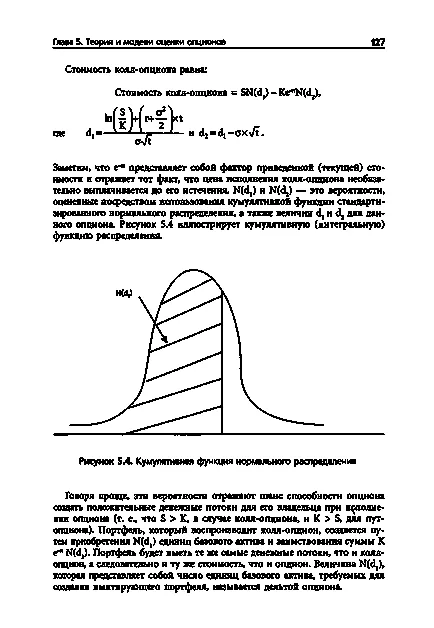
Figura 5.4. Cumulativă funcția de distribuție normală
Unul dintre cele mai interesante rezultate ale modelului de stabilire a prețurilor opțiune - o probabilitate neutră la risc de neplată, care pot fi obținute pentru firmă. Modelul Black-Scholes poate fi estimată pe baza valorii cumulative funcției de distribuție normală N (d2), care este probabilitatea neutră la risc mai mare de peste K S (S> C). Modelele de evaluare a opțiunilor, această valoare este de natură să depășească valoarea activelor firmei peste valoarea nominală a datoriei. [C.1096]
Cumulative ale funcției normale de distribuție 127 Cupoane 15 [c.1301]
N (d) volatilitatea funcției de distribuție normală cumulativă v (abaterea standard anualizată) [c.407]
cumulativ Funcția normală de distribuție poate fi aproximată prin următoarea polinomul (polinomial). În primul rând, se calculează valoarea lui x. y și z. Pentru a găsi N (d) d [c.407]
Următorul pas în tabele sunt valoarea standardizată a distribuției cumulative de probabilitate normală la punctele 0.6 și 0.4. O metodă alternativă de calcul a valorilor cumulative ale funcției standard de distribuție normală de probabilitate este de a găsi un polinom care a fost explicat în Sec. 8. [c.480]
La construirea formă de regresie cumulativă F (x) a funcției de distribuție nu este de natură fundamentală, deși este cunoscut [90], având în vedere utilizată în acest caz, metoda de estimare cele mai mici pătrate obține legea de distribuție normală se potrivesc cel mai bine. [C.155]
Rețineți că e RT este un factor dat (curent) valoare și reflectă faptul că prețul de exercitare al unei opțiuni call plătit în mod necesar, înainte de expirarea acestuia. N (dj) și N (d2) - probabilitatea este estimată prin utilizarea funcției de distribuție normală cumulativă standardizată. valori și d și D2 pentru această opțiune. Figura 5.4 ilustrează cumulativ (cumulat) funcția de distribuție. [C.127]
Taylor [159] au studiat problemele legate de liste de verificare justificare economică sume cumulate ale mediei eșantion de o distribuție normală cu variație cunoscută de Scorul de calitate. Ea se bazează pe faptul că placa de control al sumelor cumulative sunt destinate procesului de detectare a schimbării punctului de formare a unei măsuri de calitate predeterminată pe presupunerea că o tulburare apare brusc cu un parametru de offset cunoscut. Timpul preconizat de tulburare presupuse cunoscute. Procesul este oprit pentru a rezolva problema. În cazul în care semnalul nu este tulburarea este eronată, este nevoie de mai mult timp pentru a găsi cauza problemei și fixați-l. Funcția de cost aproximativă pe baza următoarelor ipoteze [c.137]
Din tabele standard funcția de distribuție cumulativă a unei variabile aleatoare distribuite în mod normal, vom găsi [c.165]
N (dj) nN (d2) - probabilitatea normală cumulativă mai precis, normală cumulativă funcția de distribuție de probabilitate a valorilor densității sau cumulative de distribuție de probabilitate rms d1 și respectiv d2; luând în considerare deviația standard a acțiunilor pe o perioadă suficient de lungă de timp (s). [C.135]
N () = funcția cumulativă de distribuție a probabilității normală definită de ecuația (3.21). [C.156]
N () = normală cumulativă funcția de distribuție a probabilității [c.237]
Funcția NORMDIST () calculează distribuția cumulativă normală, iar rezultatul este un număr între zero și unu. P1 () funcția susține o matematică constantă „n“. LN () este logaritmul natural. EXP () - argumentele exponentului, un SQRT () calculează rădăcina pătrată. [C.210]
N (d) = aria de sub curba distribuției normale standard sau probabilitatea ca o distribuție normală cu o medie de 0 și abatere standard. egal cu 1, rezultatul va fi în mod corespunzător mai puțin dl și d2 (sau o altă definiție a unei funcții cumulative de densitate de probabilitate normală). Calcularea N (d) în Ex el urmează Function - "NORMRASPR (d 0 l H THHa)". [C.65]