Definirea moment de corpuri de inerție Overbeck pendul
DEFINIREA MOMENTUL inerției ORGANISMELOR
PRIN Overbeck pendul.
Scop - determinarea momentului de inerție al sistemului de patru mase m identice de marfă în două moduri: 1) experimental folosind Oberbeck pendul 2) teoretic, luând în considerare o mulțime de puncte materiale. Comparați rezultatele.
Instrumente și accesorii. Overbeck pendul, cronometru, bar la scară, un set de bunuri, șubler.
Momentul de inerție - o cantitate fizică ce caracterizează inerția de rotație a mișcării corpului.
Momentul de inerție al punctului material al axei de rotație este produsul masei punctelor de pe pătratul distanței față de axa (a se vedea. Fig. 1)
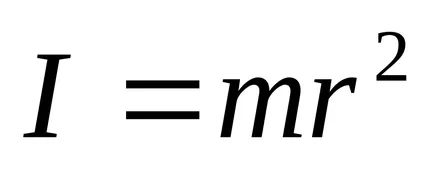

Momentul de inerție în raport cu o axă arbitrară este suma momentelor de inerție ale punctelor de masă care alcătuiesc corpul, această axă (vezi. Fig. 2)
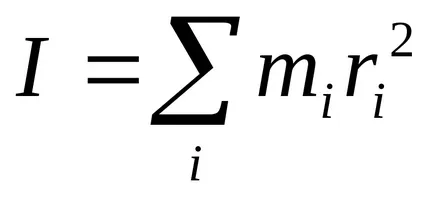
Pentru corpuri omogene de formă geometrică regulată poate înlocui însumării prin integrare.
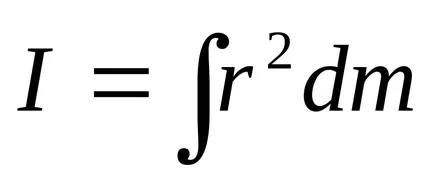
unde dm = ρdV (ρ - substanțe densitate, dV - elementul de volum)
formula astfel obținut a unor organisme m în masă în raport cu o axă care trece prin centrul de greutate:
a) lungimea tijei
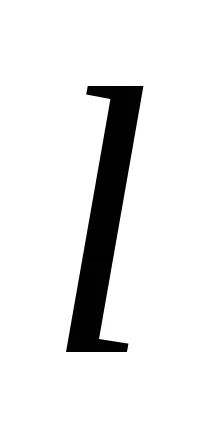
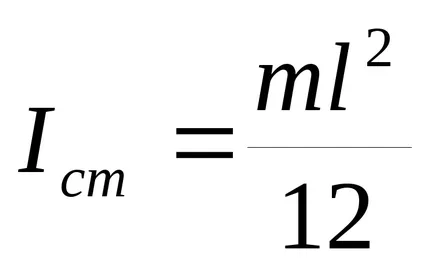
b) inelul (precum și un cilindru cu pereți subțiri) în jurul unei axe perpendiculare pe planul cercului și care trece prin centrul de greutate (care coincide cu axa cilindrului)
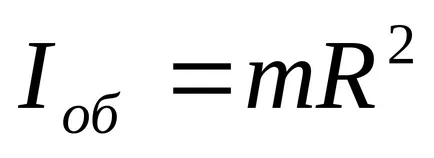
unde
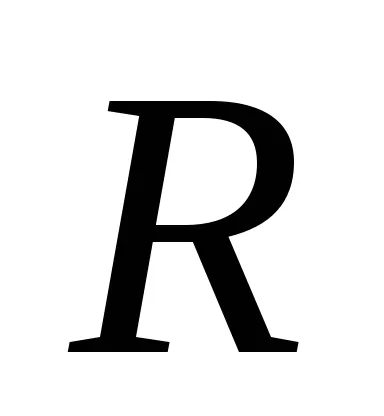
c) discul (cilindru solid) în raport cu o axă perpendiculară pe planul discului și care trece prin centrul de greutate (care coincide cu axa cilindrului)

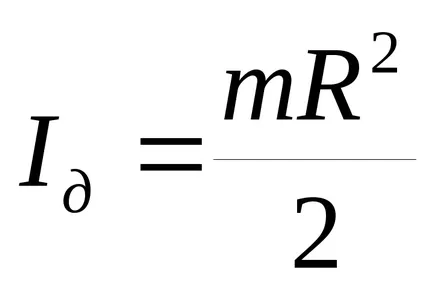
unde
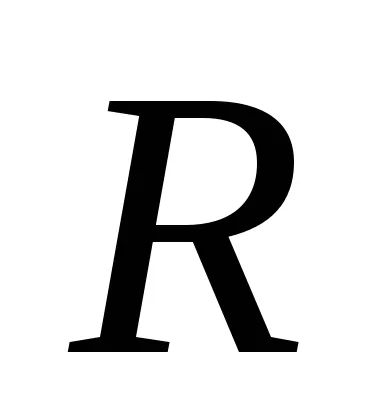
g) o sferă de rază R în jurul axei de direcție arbitrară care trece prin centrul de greutate

Momentul de inerție depinde de: 1) forma și dimensiunile corpului, 2) distribuția masei și masă, 3) din poziția axei în raport cu corpul.
Teorema lui Steiner în jurul unor axe paralele scrise ca:
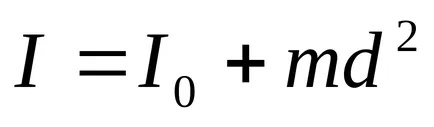
unde
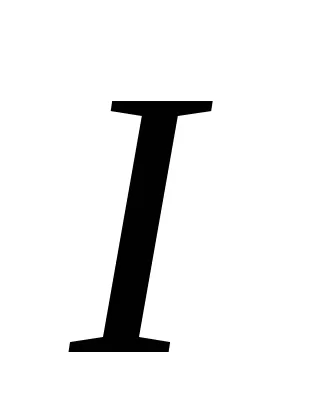
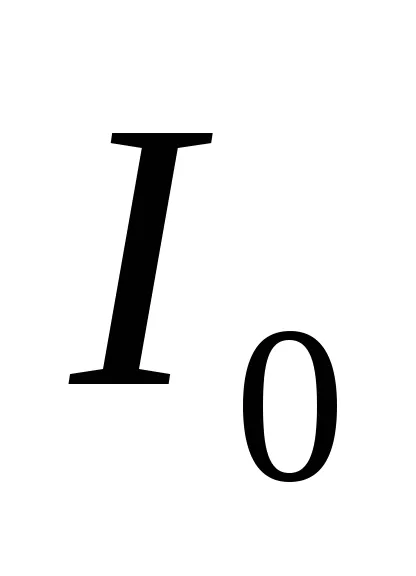

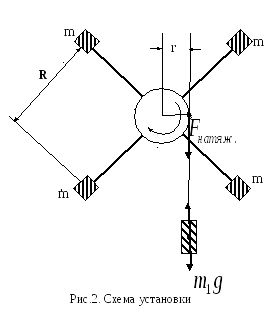
Overbeck pendul este un păianjen care constă dintr-un scripete și patru egale tije fixate pe axa orizontală (vezi. Figura 2). Pe tijele de la distanțe egale de axa de rotație
Scriem doua lege a lui Newton pentru care se încadrează de încărcare în formă vectorială

unde
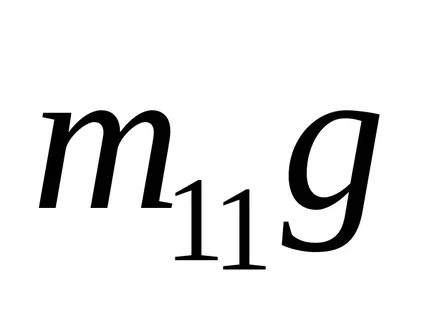
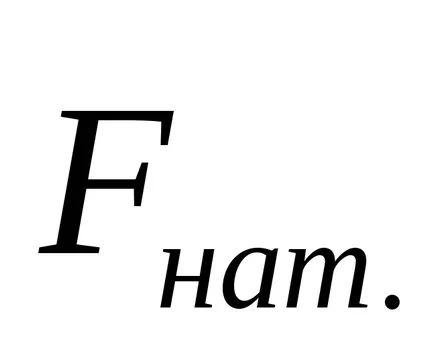

Luând direcția de deplasare a sarcinii este pozitivă, rescriem ecuația (I) în formă scalar
în cazul în care obținem expresia pentru forțele de tensiune șir
Linear accelerații este determinată de formula căii de mișcare uniform accelerată fără viteză inițială
unde h - înălțimea de m1 picătură de transport maritim; T - timpul de toamna.
forța de tensionare a firului Fnat determină rotirea rapidă a crucii. Legea fundamentală a mișcării de rotație a crucii, ținând seama de forțele de frecare poate fi scris ca:
unde M - momentul în care forța de strângere; Mtr - cuplul de frecare; I - momentul de inerție al crucii; i - accelerația unghiulară, care se rotește cruce. Magnitudinea momentului forțelor de frecare Mtr în comparație cu valoarea cuplului M este mic și, prin urmare, pot fi neglijate.
Din ecuația (5) de mai sus de finalitate remarca Achiziționați ing o formulă de calcul a momentului de inerție al crucii
unde r - raza rolei. accelerația angulară se determină din formula i
Substituind (3) și (7) în (6) obținem formula finală pentru calcularea momentului de inerție al broaștei
Ordinea de performanță.
Determinarea experimentală a momentului de inerție 4hgruzov.
1. Scoateți din miezurile sarcini m.
2. rănii într-un strat al cablului de pe scripetele, sarcina pe setarea-m1 clorhidric preselectat înălțime h. Eliberarea bara transversală, măsoară timpul să renunțe la marfă Pomo-schyu cronometru. Experiența repetată de cinci ori (la aceeași înălțime Pada-TION h).
3. Fixați capetele tijelor încărcări m.
4. Se efectuează operațiile prevăzute la alineatul 2, un cronometru de măsurare care se încadrează timp t. Experiența de a repeta de cinci ori.
5. Folosind șublere, măsurați diametrul fuliei d până la cinci poziții diferite.
6. Rezultatele măsurătorilor înregistrate în tabel. Găsiți valori aproximative si Student metoda evalua valori absolute la eroarea de măsurare, t și d.
7. Conform formulei (4) pentru a calcula valoarea accelerației liniare a, care scade m1 de sarcină pentru cazurile:
b) de bază cu încărcături de (a).
8. Conform formulei (8) pentru a calcula momentul de inerție al crucii fără încărcătură (Io) și sarcini (I), folosind valorile aproximative ale m1, R, g, iar valorile obținute a și ao.
Se calculează incertitudinea de măsurare a următoarelor formule:
Rezultatele măsurătorilor și a calculelor
1. Teoretic găsi momentul de inerție al sistemului încarcă masa 4 x m, la o distanță R față de axa de rotație (presupunând sarcini puncte materiale)
2. Comparați rezultatele experimentului și calcule. Scădeți eroarea relativă
și pentru a trage o concluzie cu privire la cât de mare diferența rezultatelor.
1. Ceea ce se numește momentul de inerție al punctului material și un corp arbitrar?
2. Ce determină momentul de inerție al corpului în raport cu axa de rotație?
3 furnizează exemple de formule corpuri de inerție. Cum au obținut?
4. Steiner teorema axelor paralele și utilizarea practică.
5. Formula Concluzie pentru calcularea momentului de inerție al crucii cu și fără sarcină.
1. Savelev I. V. Curs de fizică generală: formare. ajutor pentru colegii tehnice :. 3 tone Vol.1: Mecanică. Fizica moleculara. - 3rd ed. Corr. - M. Nauka, 1986. - 432s.
2. Detlaf A. A. Yavorsky BM Fizică Curs: formare. ajutor pentru colegii tehnice. - M. Școala Superioară, 1989. - 607 p. - piese. decret. a. 588-603.
3. Zisman G. A. M. Todes generală Fizică Curs pentru universitățile tehnice: 3 TT 1: Manual, Fizica Moleculara, Waves - 4th ed .. stereotip. - M. Nauka, 1974. - 340 p.
4. Instrucțiuni metodice lucrări de laborator la rubrica "Mecanică" .- Ivanovo, IHTI, 1989 (editat de Birger BN).