Viteza de fază și grup de lumină
Deoarece indicele de refracție și, prin urmare, viteza luminii depinde de frecvența și orice lumină nu este strict monocromatică, se pune întrebarea cu privire la ceea ce se înțelege prin viteza de propagare a semnalului luminos măsurat experimental.
Toate receptoarele răspund la energia luminii, astfel încât în toate experimentele rata de transfer de energie este măsurată printr-un semnal luminos; aceasta se numește viteza de grup și. Aceasta diferă - de viteza de propagare de fază (viteza de fază) νφ, care este determinată exclusiv de valoarea calculată și partea reală a indicelui de refracție. Departe atât regiunea de dispersie a vitezei aproape coincid.
Pentru a clarifica aceste concepte, ia în considerare două valuri cu amplitudine egală și frecvențe relativ apropiate:
Acum, să ne imaginăm un observator care se mișcă cu valuri și l uitam în aceeași fază. Pentru acest observator următoarea condiție:
iar viteza sa este egală cu viteza de fază a undei este,
Dacă un alt observator se va muta împreună cu maxim „grup val“ de amplitudine (.. Adică energia maximă), următoarea condiție pentru ea:
și viteză (grup) este
Notând că între derivata numărului de undă k și derivatul de lungime de undă (în mediu) există o relație:
obținem relația dintre grup și viteza de fază:
Astfel, viteza de grup poate coincide cu faza (fără dispersie), este mai mică decât faza (dispersia normală) sau mai mare decât (în dispersie anormală). Cu toate acestea, putem arăta că, în conformitate cu teoria relativității a vitezei de grup nu depășește viteza luminii în vid:
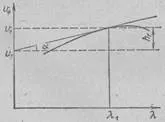
Menționăm, în concluzie, că, în dispersia puternică a conceptului de grup și de fază vitezele nu sunt suficiente pentru o descriere corectă - propagare a undei. Dar nu ne vom angaja în rafinament în continuare. P. Ehrenfest a propus un mod elegant de a găsi viteza de grup. Cunoscând cursul indicelui de refracție n = f (λ). puteți construi o curbă de νf = f (λ) (fig. 8.3). Având o tangentă la curba de la punctul cu coordonate λ1. Stabilim intercepta pe axa ordonatelor tangenta egală cu valoarea vitezei de grup în apropierea λ1 lungime de undă. u1 = ν1-h1 (vezi. Eq 8.8).
Moleculele (sau atomii) sub influența dielectrice câmpului undelor electromagnetice
inmultire în dielectric viteza luminii, ajunge în oscilațiile forțate și devin ele însele radiatoare secundare ale undelor, o coerente cu valul fundamental (8.9), dar sa mutat în fază. Adăugat la valul fundamental, aceste valuri produc un nou val, faza, care este, de asemenea, diferit de faza a undei fundamentale - acest lucru poate fi interpretat ca răspândirea undei sumei cu o viteză diferită de fază c.
În cazul în care unda se deplasează în dielectric calea l la o viteză în cazul în care acesta a petrecut timpul său
Dacă unda a trecut aceeași cale într-un vid cu viteza c, timpul scurs va fi egal cu t2 = l / c. Prin urmare, intervalul de timp este egal cu:
Dacă perioada de undă egală cu T, decalajul de fază va fi:
Ne arată cum, în cel mai simplu caz, se poate lua în considerare influența undelor secundare. Să presupunem că un val plan (8.9) care se extinde în direcția de creștere x, întâlnește pe drum stratul dielectric plat, fețele sale au coordonatele (x = 0 și bH). Gasim intensitatea câmpului la punctul A la coordonatele (x = A y = 0, z = 0), în care A >> λ. Acest câmp este format din câmpul undei (8.9) și câmpul suplimentar creat de dipoli de dielectric, t. E.
Pentru a calcula utiliza metoda AE zonelor Fresnel (§4.1). Câmpul de la punctul A este determinat prin acțiunea unei jumătăți a primei zone Fresnel; este un cerc cu centrul la origine pe care se sprijină conul razelor care provin din diferite puncte ale zonei și care converge într-un punct A. Lungimile acestor grinzi sunt schimbate de la A la A + λ / 2. Evident, raza zonei este
Zona Zona este S = πρ 2. Deplasarea unui cilindru dielectric, sprijinindu-se pe această zonă este egală cu S = bH Av. Atunci când concentrația de molecule N numărul de molecule per volum este indicat-N AN Av.
Moleculele dobândi momente dipol p Sub influența câmpului undei (8.9). câmp de radiație Tension dipol în planul său ecuatorial la distanța R este egală cu:
Deoarece dimensiunea regiunii de colț este foarte mic, se poate presupune că toate dipoli emit planul său ecuatorial. Distanța R în numitorul (8.12) poate fi luată ca A. Aceleași argumente pot lua distanța medie:
? Apoi, intensitatea câmpului creat la punctul A tot volumul dipoli V, este egal cu:
Adăugarea-l la intensitatea undei fundamentale a câmpului, obținem:
Din moment ce (din cauza volumului este mic), atunci puteți lua:
Astfel, întârzierea de fază este egală cu:
Dar, după cum este bine cunoscut (a se vedea. „Electricitate si magnetism», § 1.9),
Noi nu iau în considerare interacțiunea dipoli unele cu altele, care este permisă numai la concentrații scăzute de molecule, de ex., E. Pentru gaze. Dar, în același timp, n diferă puțin de unitate, și pot fi luate
Prin urmare, (8.15) urmează expresia finală pentru trecerea de faza:
Această expresie este diferită de expresia exactă (8,10) doar printr-un factor π / 2 aproape de unitate. Apariția acestui factor explică calculul simplificat (a fost necesar să se integreze dipoli pe teren și am luat valoarea medie și înmulțit cu numărul de dipoli).
Astfel, mecanismul de întârziere descrise mai sus au condus la o adevărată estimare a defazajului.