Vereina l

= V ¥ mv + r ¥ ma = 0 + r ¥ F = M O.

Dacă la un punct material, există mai multe forțe, M O trebuie văzută ca un moment rezultantei lor.

dL O dt = Â M iO.

care exprimă teorema de schimbare a momentului cinetic al unui punct în raport cu centrul de material:

derivata vectorului momentului cinetic al punctului material în raport cu un centru este egală cu suma geometrică a momentelor forțelor care acționează asupra punctului, în raport cu același centru.

Acestea din urmă dependență poate fi scrisă în proiecții pe axele de coordonate:

dl ix x dt = Â M; dL y dt = Â M iy; dL z dt = Â M iz.

Aceste ecuații reprezintă teorema de schimbare a momentului cinetic în jurul punctului axei:

derivata a momentului cinetic al unui punct material în jurul unei axe egală cu suma algebrică a momentelor forțelor care acționează asupra punctului în raport cu aceeași axă.

Corolarul Teorema. 1. Dacă linia de acțiune a forțelor rezultante aplicate materialului în orice moment trece printr-un anumit centru, momentul cinetic al unui punct material rămâne constantă în raport cu acest centru.

În acest caz, puterea F - este întotdeauna direcționată de-a lungul vectorului raza punctului - -

ki B (figura 1.64, b.), prin urmare, produsul vectorial al r - ¥ F

și, prin urmare, L - C = const.

2. În cazul în care momentul rezultant aplicat punctului material al forțelor în jurul unei axe, în orice moment egal

zero, momentul cinetic al unui punct material relativ la această axă rămâne constantă. egală cu zero, adică. e. momentul forței F în raport cu punctul C este egal cu zero,

De exemplu, dacă S M IV = 0, prin urmare, dl y / dt = 0 și y = L

1.20. Teorema MODIFICARE momentul cinetic MECANICĂ SISTEME

moment unghiular cinetic al sistemului mecanic relativ la un anumit centru de apel un vector egal cu suma geometrică a momentului cinetic al punctelor materiale ale sistemului în raport cu acest centru.

Momentul cinetic cinetică a sistemului mecanic este, de asemenea, numit impulsul unghiular principal al sistemului mecanic. De exemplu, în ceea ce privește un centru în ea va fi calculată după cum urmează:

L B = Â L iB = Â (r i ¥ m i v i).

în care r - - vector raza i-lea punct material în raport cu centrul în i; m i v - i - cantitatea de deplasare a unui punct material.

Impulsul sistemului în raport cu axa egală cu suma algebrică a momentului cinetic al punctelor materiale incluse în sistem, în raport cu aceeași axă.

De exemplu, în ceea ce privește axa Oz

Să considerăm un sistem mecanic format din puncte materiale k. Puncte materiale sunt în mișcare sub acțiunea

unei forțe interne F i J externe i F E și. Pentru fiecare punct de material de pe centru fix selectat O pe baza teoremei de schimbare a unghiulare scrie impuls

d L iO = M iO E + M iO J.

K obține astfel de ecuații; suma:

 dt d L iO =  M iO E +  M iO J.

După cum sa indicat anterior (a se vedea. Sect. 1.12), toate forțele interne de moment principale despre orice centru este egal cu zero, adică. E.

 M iO J = 0. Atunci

 dt d L iO =  M iO E sau dt d  L iO =  M iO E.

Această ecuație este o teorema privind schimbarea momentului cinetic al unui sistem mecanic:

derivata a vectorului momentului unghiular în raport cu un sistem mecanic este centrul principalelor momente ale forțelor exterioare care acționează asupra sistemului, în raport cu același centru.

egalitate Vector meci de egalitate în trei proiecții pe axele de coordonate:

dl x dt = M x E; dL y dt = M y E; dL z dt = M z E.

unde L x. L y. L z - momentele cinetice ale sistemului mecanic în raport cu axele de coordonate; M x E. M y E. M z E - momentele principale ale forțelor exterioare care acționează asupra sistemului aproximativ aceleași axe.

Corolarul Teorema. 1. În cazul în care momentul principal al forțelor externe cu privire la un centru tot timpul este zero, momentul cinetic al unui sistem mecanic în ceea ce privește acest centru rămâne constant:

dL - O / dt = 0, și, prin urmare, L - O = const.

Această poziție se numește legea conservării kinetichesko-

lea moment despre centrul sistemului mecanic.

2. În cazul în care momentul principal al forțelor externe, în jurul unei axe tot timpul este zero, momentul cinetic al unui sistem mecanic în raport cu axa rămâne constantă.

De exemplu, M z = 0, atunci dl z / dt = 0, și, prin urmare, L z = const.

1.21. Teorema DE MODIFICARE cineticii de energie al unui punct material

Desigur, în fizică este cunoscut, că energia cinetică a unui punct material de masă m. se deplasează cu viteza v -. egală cu jumătate din produsul din masa acestui punct de pătratul vitezei sale:

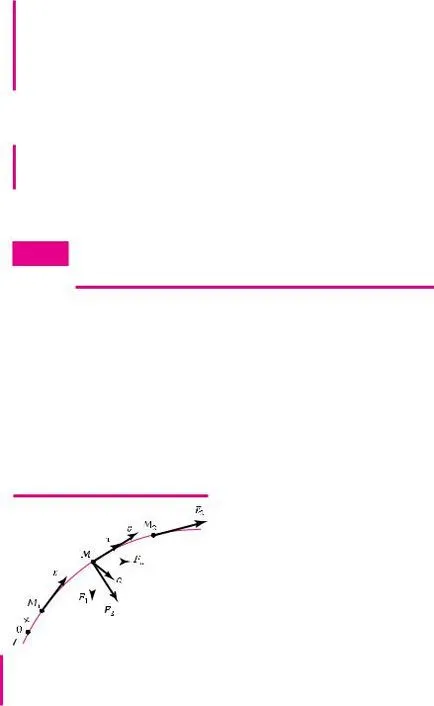
Să considerăm mișcarea punctului M prin acțiunea forțelor aplicate la acestea sisteme F - 1. F - 2. ..., F - (. Figura 1.65) n. Alegeți o direcție pozitivă de referință și scrie ecuația de bază a dinamicii

Aici, forța F - F este rezultanta unui sistem de forțe convergente - 1. F - 2. ..., F - n. Noi prognozăm vectorul este egal cu t-axa:

Valoarea obținută accelerația tangențială în ecuația de mișcare de-a lungul vectorului unitate t -.

m v d v dS = F t și m v d v = F t dS. sau d (m v.2 februarie) = cos fds (F. t).

Partea stângă a acestei ecuații este cinetică punct diferențială de energie și partea dreaptă - operația elementară pe Ds deplasării rezultante (operație efectuează numai componenta tangențială a forței rezultante):

d (m v.2 februarie) = d A.

Deoarece F t = Â F i t. și deplasarea punctului de aplicare a forței la toate aceeași, că d A = Â d A i. Prin urmare, putem scrie diferențial energia cinetică într-un alt mod:

d (m v.2 februarie) = Â d A i,

t. e. diferențială de energie cinetică de puncte elementare egal cu suma de lucrări ale forțelor aplicate la punctul.

Atunci când se deplasează de la punctul M la punctul M viteză poziția v - v - 1, Feb.

Acesta va varia de la 1 la 2; În acest caz, modificați energia cinetică

m v 2 2 2 - m v 1 2 2 = Â d A i.

Ecuația rezultată este teorema de punct material schimbare energie cinetică:

energia cinetică a schimbării materialului în termenii pe unele dintre cilindree egală cu suma algebrică a activității tuturor active la acest punct de forțe pe aceeași mișcare.

Dacă suma forței de muncă este pozitivă, atunci v 2> v 1. t. E. cinetici crește energia. În cazul în care aceeași cantitate de muncă este negativ, atunci energia cinetică scade.

1.22. Ecuațiile diferențiale ale mișcării de translație SOLIDE

În timpul deplasării spre înainte a unui corp rigid, toate punctele sale muta precum și centrul de masă, astfel încât ecuațiile diferențiale ale mișcării centrului de masă descrie mișcarea de translație a corpului:

În cazul în care m - masa corpului rigid; x C. y C. z C

Centrul Nia de masă a corpului pe axele de coordonate; F ix E. F iy E. F iz E - proiecția forțelor exterioare aplicate pe corpul rigid, axele relevante.

1.23. Ecuația diferențială a mișcării de rotație a unui corp rigid în jurul unei axe fixe

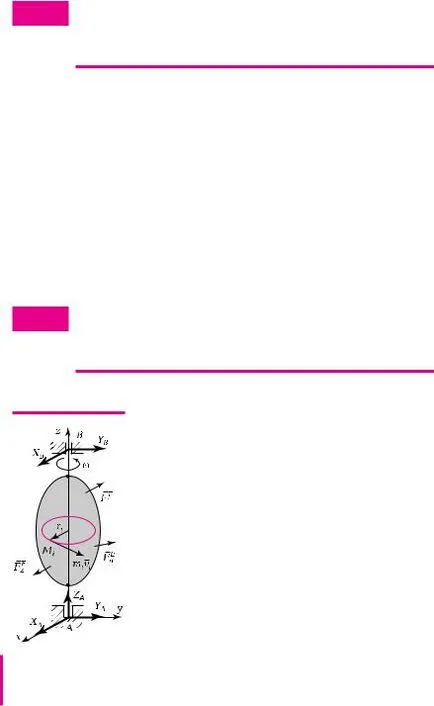
corp solid se rotește în jurul unei axe fixe sub acțiunea forțelor externe F - i E (figura 1.66). Cu o viteză unghiulară w. impulsul său unghiular în raport cu axa A z este egal cu suma momentului cinetic de puncte materiale în raport cu aceeași axă, adică. E.

L z = Â m i v i r i = Â m i w v i r i = Â m i w r i 2 =

= W Â m i r i 2 = w J z.

Astfel, am arătat că momentul cinetic al unui corp rotativ relativ rigid cu axa fixă ​​este egală cu produsul dintre momentul de inerție în raport cu aceeași axă la o viteză unghiulară a corpului:

În conformitate cu teorema de schimbare a momentului cinetic despre axa derivata de scriere a momentului unghiular în jurul axei Az

dL z dt = Â M iz E sau d (J z w) dt = Â M i E z.

J z d w dt = Â M iz E sau J z e = Â M iz E.

Dat fiind faptul că accelerația unghiulară e reprezintă derivata a doua a rotației corpul unghiului j, relația rezultată poate fi scrisă astfel:

J z j = Â M i E z.

Rezultatul este o ecuație diferențială a mișcării de rotație a unui solid în raport cu o axă fixă. Trebuie amintit că partea sa dreaptă - acesta este principalul punct extern forță predeterminată F i E. un timp de reacție de obligațiuni în raport cu axa Az este egală cu zero, deoarece reacțiile încrucișate Az axe:

În cazul în care momentul principal al forțelor externe față de axa de rotație este zero, momentul cinetic al sistemului rămâne constantă:

În acest caz, dacă este momentul de inerție al sistemului este neschimbat, sistemul este rotit cu o viteză unghiulară constantă. Dacă vom schimba momentul de inerție, viteza unghiulară se va schimba, de asemenea:

J z 1 w 1 = J z 2 w 2.

1. Ce este un organism absolut solid?

2. Ce sisteme de forțe sunt echivalente?

3. Care este principiul de corp rigid detașabil conexiunile?

4. Ceea ce deosebește activ de forțele pasive?

5. Ceea ce se numește plane sau spațiale sistemul de forțe?

6. Care este diferența convergente forțelor de locație arbitrară cu conjugat în spațiu?

7. Cum este cuplul în jurul punctului?

8. ecuațiile de bază din registrul de echilibru a unui sistem arbitrar al forțelor spațiale.

9. Care este vectorul principal al forțelor și ceea ce este? Are vectorul principal al forțelor cu privire la alegerea de a aduce centrului?

10. Metode Lista de determinare a poziției centrului de greutate al corpului rigid.

11. Are accelerația unui punct material în mișcare uniformă într-o traiectorie curbată?

12. Poate puncte ale corpului, se deplasează în mod constant, pentru a avea Cree volineynye traiectoria?

13. Care este viteza instantanee a centrului unei figuri avion?

14. În cazul în care un pasager este în cabină în direcția de zbor, viteza sa în raport cu Pământul va fi mai mult sau bărbați Chez decât viteza aeronavei?

15. Care este mișcarea corpului se va face prin adăugarea a două mișcări de rotație, în care viteza unghiulară a unui kovye și direcții diferite?

16. Notați legea fundamentală a dinamicii.

17. Care este lucrarea forței de gravitație? Are depinde de tipul de traiectoria punctului de aplicare a forței?

18. Definirea eficienței. De ce a pus acest concept?

19. Cum se determină centrul de greutate al vehiculului?

20. Se determină cantitatea de mișcare a greutății roților G și raza

R. rulare pe șină rectilinie, fără alunecare cu w viteza unghiulară.

21. În orice locație, cantitatea de masă de mate vector de mișcare indică momentul său în jurul axei va fi egal cu zero?

22. În ce condiții este momentul cinetic subiectelor UTI mecanice în raport cu centrul rămâne constantă?

23. De ce să se oprească, filare rapid skater să patineze aruncat mână în mână?