Utilizarea Excel pentru a rezolva un sistem de ecuații prin metode grafice - studopediya
Rădăcinile ecuației sunt valorile graficului punctelor de intersecție cu axa orizontală. Sistemul de ecuații este punctul de intersecție a graficelor de funcții. Această metodă se numește constatare rădăcină grafică.
Cu ajutorul procesorului de masă poate rezolva ecuații și sisteme de ecuații. Pentru soluții grafice adecvate diagrame.
Să considerăm un exemplu specific.
Găsiți o soluție la următorul sistem de ecuații:
Răspunsul este să scrie până la 0,1.
Transformarea sistemului:
1. Pentru a evalua soluțiile pe care le folosim diagrama în care afișează graficele celor două funcții. În acest scop, pe foaia de lucru MS Excel creează un tabel cu următoarele valori (a se vedea figura 1):
· 1 line - antetele de linie;
· Coloana A: umple celula A2: A22 numere -10-10 în trepte de câte 1;
· La umplerea coloanei B celula B2 formula skid = A2 * A2. care este apoi copiat B22 celule;
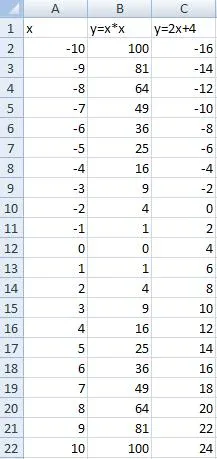
Figura 1 - Date Tabelul pentru aproximarea căutării de soluții
· La umplerea unei celule în formula coloana C skid C2 = 2 * A2 + 4, copiați-l la celula C22.
Folosind diagrame de master va alege tipul de diagramă și diagramă grafic construct efectuarea evaluării inițiale (figura 2).

Figura 2 - Schema inițială de soluții de evaluare
În figura 2 se poate vedea coordonatele punctelor de intersecție a graficelor - soluții de sistem. Cu toate acestea, în timp ce noi avem doar valori aproximative ale soluțiilor.
Pentru a verifica valorile soluțiilor construi intervale grafice -2-0, unde prima soluție, și de la 2 la 4, în care a doua soluție este la un pas de 0,1 (Figura 3).


Figura 3 - Tabelele cu datele pentru decizii ulterioare
2. Se aduce un nou tabel - 2 ≤ x ≤ 0. Clădire diagramă de dispersie pentru prima soluție (Figura 4).

Figura 4 - primele soluții de căutare
3. Asigurați-un nou tabel 2 ≤ x ≤ 4. Construirea o diagramă de dispersie pentru a doua soluție (Figura 5).

Figura 5 - Căutare pentru a doua soluție
Solutia sistemului nostru sunt coordonatele punctelor de intersecție ale graficelor: x1 = -1,25; y1 = 1,5; x2 = 3,2; y2 = 10,8.
Soluție grafică a unui sistem de ecuații sunt aproximative.