Teorema Coriolis despre adăugarea de accelerații

Acasă | Despre noi | feedback-ul

. în care - accelerația Coriolis (accelerație Coriolis) - în cazul în mișcare de translație nepostupatelnogo accelerație absolută = suma geometrică a portabilului și accelerațiile relative Coriolis. accelerația Coriolis se caracterizează prin: a) schimbarea magnitudinea și direcția unui punct de viteză portabil datorită mișcării sale relative; b) o schimbare în direcția vitezei relative a punctului de mișcarea de rotație a portabilului.

Amploarea și direcția accelerației Coriolis.

Koreolisovym sau povrotnym numit accelerare compune obsoljutno punct de accelerare în mișcare complexă, care este egală cu de două ori viteza unghiulară a produsului vectorial al rotației relative a vitezei punctului portabil

accelerația Coriolis se caracterizează prin: 1) o modificare a mărimii și direcției vitezei de translație în ceea ce privește mișcarea relativă; 2) o schimbare în direcția vitezei relative a punctului de mișcarea de rotație a portabilului. Modul accelerație Coriolis:

ac = 2 × | am × vr | × sin (ne ^ vr), vectorul de direcție este determinată conform regulii produsului vectorial sau regula Zhukovskogo: proiecția vitezei relative într-un plan perpendicular pe viteza unghiulară portabil, este necesar să porniți 90 în direcția de rotație.

Coriolis USK. = 0 în trei moduri: 1) ne = 0; în cazul mișcării de translație progresive sau la momentul tratamentului cărbunelui. Viteza 0; 2) vr = 0; 3) sin (am ^ vr) = 0; Ð(Noi ^ vr) = 0, când VR relativă de viteză este paralelă cu axa de rotație a portabilului. În cazul deplasării într-un singur plan - unghiul dintre vr

19. planșete paralel (sau plană) se numește o mișcare a unui corp rigid, în care toate punctele sunt deplasate în planuri paralele cu un plan fix. Dacă țineți linia dreaptă a corpului perpendicular pe planul fix (fig. 1.10), atunci toate punctele de pe această linie va avea aceeași traiectorie, viteza și accelerația se misca inainte. Prin urmare, pentru a studia mișcarea întregului corp este suficient pentru a studia ca S deplasează corp secțiune paralelă cu planul fix. Poziția secțiunii transversale la un moment dat este complet determinată de poziția segmentului AB (a se vedea figura 1.10, b ..), care, la rândul său, poate fi setat în trei dimensiuni:

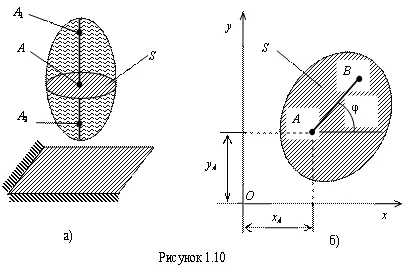
Aceste ecuații numite în funcție de mișcare plan-paralel al unui corp rigid.

Ecuațiile de mișcare a unei figuri plane.

Ecuațiile mișcării plane:

Ecuațiile de mișcare a unei figuri plane.

# 969; = d # 966; \ dt, # 949; = d # 969; \ dt = d 2 # 966; \ dt 2