sisteme de ecuații liniare în Excel Rezolvarea

2. Operații cu matrici în Excel

1) MDETERM (matrice) - calcularea determinantului matricei, 2) ASI (matrice) - calculul matricei inverse, 3) MMULT (matritsa1; matritsa2) - un produs de matrici, 4) TRANSPOSE (matrice) - transpune matrice.

Primul dintre aceste funcții ca rezultat returnează numărul (determinantul), ca o formulă poetomuvvoditsya convențională (ENTER).

Prin urmare, ultimele trei celule unitare de retur trebuie administrată ca o matrice cu formula (CTRL + SHIFT + ENTER).

Luați în considerare zadachuresheniya SLAE următorul exemplu

X 8 x 01 februarie 02 august x 24 martie

X 2 x 1 10 februarie 03 februarie x 48

X 2 x aprilie 1 august 2 x 18 martie.

Coeficienții de matrice ale necunoscutelor A (3) are forma

O formulă similară (MDETERM = (A3: C5)) pentru calcularea determinantul matricei A este scris în celula E8. Rămâne să găsească o soluție la sistem. Formulele corespunzătoare pot fi scrise în Excel B7 interval soluții: B9 în care și vezi rezultatul (figura 4) (Figura 3.).

Notă (fig. 3), care, la calcularea x i (i = 1, 2, 3)

analizează valoarea determinantul matricei sistemului A. calculat în celula E8. și dacă este zero. B7 plasat în textul „nici o soluție“, iar în celula B8 și B9 - linii goale.

3. Decizia Slough folosind Solver instrument

O clasă largă de probleme industriale cuprind problema optimizării. Probleme de optimizare sugerează valori de căutare pentru argumente care funcționează, care se numește ținta. valoarea minimă sau maximă în prezența oricăror constrângeri suplimentare. Excel are un instrument puternic pentru rezolvarea problemelor de optimizare.

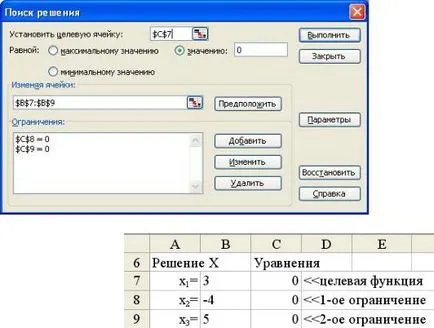
Acest instrument de add-in numit Solver (Solver)

(Disponibil din meniul Tools  Solver).

Problema de rezolvare a sistemelor liniare poate fi redusă la o problemă de optimizare.

Care dintre ecuațiile (de exemplu, mai întâi), luate ca funcția obiectiv, iar n restul de -1 considerate ca limitări.

Scriem sistemul (1) ca

o 11 x 12 x 1 2 1 a n x n b 1 0,