Sarcini pentru decizia independentă
Derivata unei funcții și aplicațiile sale
Incrementarea argumentului și incrementarea funcției
Având în vedere o funcție. Fix o anumită valoare. Să ne dea o creștere variabilă arbitrară. La punctul funcția va fi setată. Diferența dintre noua valoare a funcției și a valorii sale vechi numit incrementul funcției și este notat. Astfel, incrementul funcției este valoarea
.
Să. atunci. găsit:
=.
2.2. Conceptul de derivat.
Să - funcție arbitrară re variabilă x. Reparăm o valoare a argumentului x și se calculează valoarea corespunzătoare a funcției. Să ne dea incrementarea argumentului. Vom obține un nou set de valori și se calculează incrementul corespunzătoare a funcției. să elaboreze atitudine
și ia în considerare limita
.
Această limită se numește derivata funcției y = f (x) la x, și este notată y“. u'x. f „(x) sau mai puțin. Astfel, derivatul se numește limita incrementelor raportul unei funcții la incrementarea argumentului, unde incrementul argument tinde la zero.
Funcționarea găsi derivata unei funcții se numește pe diferentiere această funcție.
semnificația geometrică a derivatului
Să presupunem că funcția y = f (x) are un derivat de la un punct x0. Apoi, un grafic al funcției în punctul M0 (x0. Y0) poate trage o tangentă, ecuația este de forma
,
În această ecuație = tga - unde a - unghiul de înclinare a tangentei la axa x.
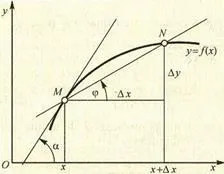
Astfel, geometrica derivat este panta tangentei la curba-TION la punctul considerat.
Sensul fizic al derivatului
Să se mută punctul de la o linie dreaptă, astfel încât aceștia - calea parcursă de un punct la momentul t. Apoi drumul parcurs de punctul în intervalul de timp Dt de la t la timpul t + Dt. este DS = f (t + Dt) -f (t). În acest caz,
este viteza medie a punctului în intervalul de timp de la t la t + Dt.
Viteza punct în acest moment este limita de viteza medie pe durata unui interval de timp Dt. și anume
(1.2) și definiția derivatului (1.1) rezultă că. și anume derivat al căii în raport cu timpul în mișcare rectilinie este viteza.
Reguli de calcul al derivatelor
Următoarele formule exprimă reguli conductive cantitatea de diferențiere, produs, funcțiile Quotient și calcularea derivata unei valori constante.
1) Derivatul de mărime constantă egală cu zero:
2) Suma derivat egal cu suma derivatelor:
.
.
3) Produs Derivative:
.
.
4) Constanta poate fi luată ca un semn al derivatului:
.
Această regulă este o consecință a regulilor 1) și articolul 3).
.
5). Derivata privat:
.
Aici se presupune că valoarea considerată a numitorul nu este zero.
=
=.