Punct feroelectric Curie

Feroelectricilor ea dielectrici, care au mai multe proprietăți specifice care sunt realizate datorită faptului că acestea au structura de domeniu într-un anumit interval de temperatură poate fi polarizata spontan, direcția de polarizare poate fi modificată de un câmp electric.

În anumite substanțe solide și lichide, în anumite impacturi externe transformări de fază apar fără a schimba stările de agregare. De exemplu, feroelectric poate fi convertit la paraelectric.

Care este punctul Curie

Dacă feroelectric ridica temperatura la o anumită temperatură ($ T_k $), care este diferit pentru fiecare substanță, proprietățile dielectrice ale feroelectrice dispare și devine un izolator obișnuit. Acest punct al fazei de tranziție de la starea feroelectric la un stat numit polar punct dielectric Curie și temperatura corespunzătoare ($ T_k $) - temperatura Curie. Sunt feroelectricilor, în care două din punctul Curie, în partea de sus și de jos. Astfel de materiale își păstrează proprietățile feroelectrice într-un interval de temperatură, care predeterminate limitele superioare și inferioare. Astfel feroelectricilor nu sunt relativ mult. Cele mai multe feroelectricilor numai punctul Curie superior.

Un grafic al polarizării spontane a feroelectric ($ P_S $) a temperaturii în apropierea punctului Curie este prezentată în Fig.1.

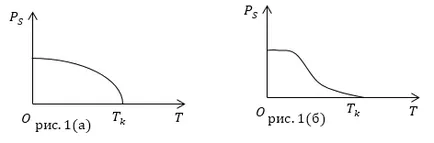
In imediata apropiere a tranziției de fază (la punctul Curie) Structura materialului feroelectric este maleabil la influențe externe. Chiar și mici schimbări în intensitatea câmpului în apropierea fazei de tranziție, care cauzează modificări substanțiale ale proprietăților electrice ale dielectric.

Lângă punctul Curie din feroelectricilor care se află în faza polară, valorile permitivității ating valori foarte mari (până la $ 4 ^ \ ^ 5) $. De exemplu, titanat de bariu $ (BaTiO_3) $ Curie Temperatura punctului este de aproximativ 120 $ ^ $ oC, iar constanta dielectrică ajunge la maximum de $ $ 6000-7000. Trebuie remarcat faptul că există feroelectricilor și constantă dielectrică nu este foarte mare, de exemplu, anumite feroelectricilor solubili în apă au o permeabilitate $ \ varepsilon = 5-6 $.

Mai mult decât atât, constanta maximă dielectrice la punctul Curie este atins (Figura 2).

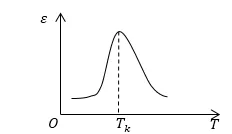
Legea schimbării a susceptibilității dielectrice

Legea schimbării a susceptibilității dielectrice a fazei feroelectrice în nepolar cu privire la punctul Curie poate fi scris ca:

în cazul în care $ A $ - constantă. $ T_0 $ - temperatura Curie - temperatura Weiss aproape de punctul Curie ($ T_k $). Foarte des în formula (1) în loc de a folosi $ T_0 $ $ T_k $. În acest caz, în cazul în care există două din punctul Curie feroelectric, al doilea punct în apropierea legii Curie-Weiss este scris ca:

În cazul dielectricilor anizotrope scalar $ \ $ varkappa în formulele (1) și (2) se înlocuiește cu tensor $ _. $ Dependența de temperatură nu se schimbă.

În practică, feroelectric legea Curie-Weiss pot fi scrise în scopul de a găsi constanta dielectrică în forma:

unde $ C = \ frac $ - Curie-Weiss constantă, T_k $ $ - temperatura Curie la care are loc tranziția de fază, și $ \ alpha $ schimbari semn. Dacă C $ \ sim ^ 3 $, tranziția de fază are loc cu ordonarea unora dintre elemente structurale, ioni, protoni sau grupuri de atomi. O astfel de tranziție este uneori menționată ca: ordine - dezordine. Dacă C $ \ sim ^ 5 $, tranziția de deplasare în raport cu poziția de echilibru. Curie Constant - Weiss adesea determinată dintr-un grafic de $ \ frac = \ frac \ din stânga (T \ dreapta) $.

Trebuie spus că diferitele tranzițiile feroelectrice pot avea, atât prima și a doua clasă. Prin feroelectricilor cu o tranziție de ordinul întâi (. Figura 1 (a)) le includ pe cele care experiență polarizare sare la temperatură și presiune constantă:

în cazul în care $ F $ - potențial termodinamic, egal cu:

Prin feroelectricilor cu a doua fază de tranziție (Figura 2 (a)) includ dielectrici a căror sensibilitate dielectric modificări brusc la presiune și temperatură constante (?):

Prezența punctul Curie este o proprietate caracteristică a unui material feroelectric.

Sarcina: Pentru fosfat de potasiu ($ KH_2PO_4 $), care este o polarizare feroelectric care este cauzată de deplasarea ionilor de hidrogen la temperaturi nu apropiate de punctul Curie, experiența dă:

Se determină valorile unor variabile sunt prezentate în termeni de (1.1)? Găsiți raportul dintre interne câmp $ \ beta, $, folosind formula (1.2):

Ca bază pentru rezolvarea problemei va avea o formulă care determina relația dintre constanta dielectrică a feroelectric cu temperatură:

Apoi, comparând expresiile (1.3) și (1.1) obținem:

În acest caz, coeficientul de $ \ beta $ este ușor de calculat, folosind (1.2). obținem:

Raspuns: $ \ beta = 0,567 $.

Sarcina: Având în vedere două grafice de $ \ varepsilon $ (T) și $ \ frac \ din stânga (T \ dreapta) $ Figura 3 (a, b). Se determină în ce fază a feroelectric includ listele I și II.

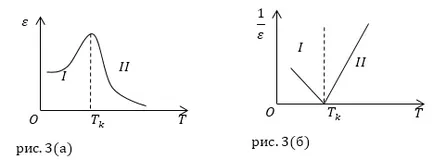
Luați în considerare graficul din fig. 3 (a). Segment al curbei marcat I numeral, corespunde fazei dielectrice feroelectric, punctul Curie ($ T_k $) polarizare atinge un segment maxim corespunde cu figura II fază dielectric paroelektricheskoy. Constantei dielectrice scade brusc odată cu creșterea temperaturii pauze în jos structura domeniului substanței.

Luați în considerare graficul din fig. 3 (b). În conformitate cu legea Curie-Weiss:

Segmentul I, se referă la faza de - feroelectrice. Inversul cu constanta dielectrică, descrește liniar cu creșterea temperaturii, până la $ T> T_k $, atunci când $ T = T_k $ $ \ frac = 0 $. Următorul segment II - paraelectric la o temperatură mai mare decât punctul Curie.