moduri neobișnuite de a se multiplica

Un bărbat în viața de zi cu zi nu se poate face fără calcul. Prin urmare, în clasa de matematică, am în primul rând, să învețe pentru a efectua operațiuni pe numere, care este considerat. Noi înmulțire, împărțire, adunare și scădere, ne-familiare tuturor în moduri care sunt predate la școală.

Într-o zi, din greșeală am dat peste cartea S. N. Olehnika, Yu. V. Nesterenko și M. K. Potapova "Vechile provocări interesante." Răsfoind această carte, atenția mea pagină numită „Multiplicare pe degete.“ Sa dovedit că este posibil să se multiplice, nu numai pentru că noi oferim un manual de matematică. Am fost curios, și dacă există încă metode de calcul. La urma urmei, capacitatea de a face rapid calcule este surprinzător de sincer.

Utilizarea constantă a tehnologiei moderne de calculator conduce la faptul că studenții consideră că este dificil de a face orice plăți fără a avea la dispoziție un tabel sau adăugarea de mașină. Cunoașterea metodelor de calcul simplificate face posibilă nu numai pentru a efectua rapid calcule simple în mintea ta, dar, de asemenea, să monitorizeze, să evalueze, să localizeze și să corecteze erorile, ca urmare a mecanizării de calcul. În plus, dezvoltarea de competențe informatice dezvoltă memoria, crește nivelul de cultură matematică de gândire, ajută să absoarbă pe deplin obiectele ciclului fizic și matematic.

Găsiți ca bolsheneobychnyh modalități de calcul.

Aflați cum să le aplice.

Pentru a alege pentru ei înșiși cele mai interesante sau mai ușoare decât cele de școală kotoryepredlagayutsyav, și să le utilizeze în cont.

Aceste metode de calcul pe care le folosim astăzi, nu au fost întotdeauna atât de ușor și convenabil. În zilele vechi am folosit metode mai greoaie și lente. Și dacă elevul a secolului 21 ar putea fi transferat la cinci secole în urmă, el ar fi lovit viteza noastră strămoșii și infailibilitatea calculelor sale. Zvonurile despre l-au răspândit prin școlile din jur și mănăstiri, eclipsează slava contori cele mai calificate ale epocii, și din toate părțile au venit să învețe de la noul Mare Maestru.

Deosebit de dificilă, în zilele de demult au fost operarea de înmulțire și împărțire. Apoi, nu mai era nimeni lucrat practica de recepție pentru fiecare acțiune. Dimpotrivă, mutarea a fost atât de aproape o duzină de diferite metode de înmulțire și împărțire - acceptarea unul de altul confuz, amintiți-vă că a fost persoană incapabilă de capacitatea medie. Fiecare profesor lucruri numărabile păstrat sale remediile, fiecare „diviziune maestru“ (au existat astfel de experți) a lăudat felul său de a efectua această acțiune.

Toate aceste metode de înmulțire - „șah sau organ este“, „prin pliere“, „cruce“, „bare“, „înapoi“, „diamant“ și alte concurau între ele și asimilat cu mare dificultate.

Să ne uităm la cele mai interesante și ușor de moduri de a se multiplica.

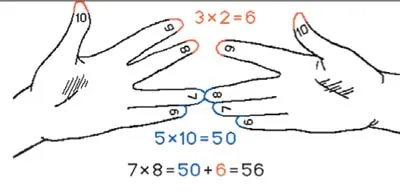
Drevnerumynsky mod de a multiplica pe degete este una dintre metodele cele mai comune care sunt utilizate cu succes de secole negustori romani. Ei au învățat să se înmulțească numere cu o singură cifră pe degetele de la 6 la 9. În acest caz, a fost de ajuns să dețină abilitățile inițiale de „unități“ deget-numărare, „perechi“, „trei“, „patru“, „cinci“ și „zece“. Degetele aici servește ca un dispozitiv de calcul auxiliar.

Pentru a face acest lucru, pe de o parte a tras cât mai multe degete în ceea ce privește primul factor depășește numărul 5, iar al doilea a făcut același lucru pentru al doilea factor. Celălalt a fost pliat degetele. Apoi a fost dus la numărul (total) degete alungite și înmulțit cu 10, numerele apoi încrucișate înmulțit arată câte degete încrețite, iar rezultatele sunt însumate.

De exemplu, se înmulțește 7 cu 8. În exemplul va fi buclat degetele 2 și 3. Dacă cantitatea degetelor îndoite pliate (2 + 3 = 5) și se multiplică numărul nepliate (2 • 3 = 6), se obține, respectiv, numărul de zeci și unități de produs dorit 56. Astfel, putem calcula produsul numerelor de cifre, mai mult de 5.

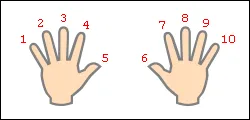
Înmulțirea numărului de 9-9 · 1, 2 ... 9 · 9 × 10 - ușor de eliminat din memorie și convertit metoda adaosului manual mai greu, cu toate acestea, numărul 9 este de multiplicare poate fi ușor de reprodus „degete“. degete Rastopyrte pe ambele mâini și rotiți mâinile, cu palmele departe de tine. atribuie Mintal degetele succesiv numerele de la 1 la 10, începând cu degetul mic de la mâna stângă și mâna dreaptă degetul mic se termină (prezentat în figură).

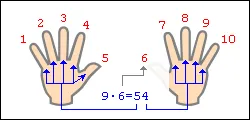
Să presupunem că vrem să multiplice 9 6. Ori degetul cu un număr egal cu numărul pentru care multiplica nouă. În exemplul nostru, trebuie să se aplece degetul cu numărul 6. Numărul de degete pe partea stângă a degetului pliat ne arată numărul de zeci în răspuns, numărul de degete pe dreapta - numărul de unități. În stânga avem 5 degete sunt îndoite spre dreapta - 4 degete. Astfel, 9 · 6 = 54. Figura următoare ilustrează în detaliu întregul principiu al „calcul“.

Un alt exemplu: trebuie să calculeze 9 × 8 =. Pe drum, spune, că, în calitate de „mașină de numărare“ nu poate acționa în mod necesar ca degetele. Să luăm, de exemplu, 10 celule într-un notebook. Crucea din celula 8-lea. De la stânga la stânga 7 celule, dreapta - 2 celule. Prafuri 9 x 8 = 72. Este foarte simplu.

Astfel, în opinia mea, „nativ“ și ușor de multiplicare fel este o metoda care a folosit țăranii români. Această tehnică nu necesită cunoștințe de tabele de multiplicare pe numărul 2. Esența este că multiplicarea oricăror două numere este redus la o serie de consecutive despărțind un număr în jumătate în timp ce dublarea numărului de altul. De împărțire în două continua atâta timp cât privat nu se va transforma 1, paralel cu dublarea atât numărul. Recent, a dublat numărul și dă rezultatul dorit.

În cazul unui număr impar trebuie să se debaraseze de o jumătate și se împarte reziduul; dar până în ultima zi a coloanei din dreapta va trebui să adăugați toate numerele din acea coloană, care stau împotriva numerele impare ale coloanei din stânga: Suma este produsul dorit

Produsul din toate perechile de numere corespunzătoare la fel, astfel încât

37 ∙ ∙ = 1184 1 32 = 1184

În cazul în care unul dintre numerele sau numerele impare sunt atât de ciudat, se procedează după cum urmează:

24 ∙ 17 = 24 ∙ (16 + 1) = 24 ∙ + 24 = 16 384 + 24 = 408

O nouă metodă interesantă de multiplicare, care au fost raportate recent. Inventatorul unui nou sistem de cont oral de doctorat Vasili Okoneshnikov afirmă că o persoană este în măsură să memoreze un magazin imens de informații, cel mai important - cum să aranjeze informațiile. În opinia savantului, cea mai avantajoasă în acest sens este sistemul nonary - toate datele este doar o nouă celule, aranjate ca butoane de pe calculator.

Considerat foarte simplu pentru un tabel. De exemplu, pentru a multiplica numărul 15647 5. În tabelul corespunzător cinci, pentru a alege un număr corespunzător numărului de cifre, în ordine: unul, cinci, șase, cvartet și Seven. Obținem: 05 25 30 20 35

Figura din stânga (în exemplul nostru - zero) și lăsați neschimbate următoarele cifre se adaugă în perechi cu primele cinci de doi, cinci dintre un triplu, zero la doi, zero la trei. Cifra din urmă, de asemenea, neschimbate.

Ca rezultat, vom obține: 078235. Numărul 78235 este rezultatul înmulțirii.

Dacă se dovedește că numărul mai mare de nouă, se adaugă prima cifră la figura anterioară a rezultatului, iar al doilea este scris la locul „lui“ în adăugarea a două numere.

Învață să contorizați toate metodele prezentate, am ajuns la concluzia că cele mai simple metode sunt cele pe care le studia în școală, acestea pot fi mai familiar pentru noi.

Din tot ce am găsit modalități neobișnuite în cont părea mult mai interesant de „multiplicare zăbrele sau gelozie.“ I-am arătat colegii lui, și ia plăcut prea.

Cea mai simplă metodă mi se părea „dublarea și divizare“, care a folosit țăranii români. L folosesc cu multiplicarea numerele nu sunt prea mari (foarte convenabil de a utiliza atunci când înmulțirea numere din două cifre).

Mi-a interesat un nou mod de multiplicare, deoarece permite mintii sa „rostogoli“ un număr foarte mare.

Cred că modul nostru de multiplicare într-o coloană nu este perfectă, și puteți veni cu moduri chiar mai rapid și mai fiabile.

I. Depman „Povești de matematică.“ - Leningrad. Educație, 1954. - 140 p.

Olehnik S. N. Nesterenko V. Potapov MK "Vechile provocări interesante." - M. Science. Ediția Casa Literaturii Fizică și matematică, 1985. - 160 p.

Perelman YI Contul Rapid. Treizeci de tehnici simple de conturi orale. L. 1941-1912.