mișcare plan de descompunere a unui corp rigid și translație de rotație la pagina 2

Accelerația punctul Aba B primește de rotație în jurul stâlpului A, componentele accelerației sunt determinate după cum urmează:

Instantaneu centrul de accelerare. În fiecare moment al mișcării unei figuri plane în planul său, iar dacă w e nu sunt zero în același timp, există un punct unic de această cifră, accelerația este egală cu zero. Acest punct este numit centrul instantaneu al accelerației, vom nota Q.

Să ne cunoaștem în magnitudinea și direcția accelerației oricărui plan figura (punctul D), viteza unghiulară și accelerația unghiulară a figura e.

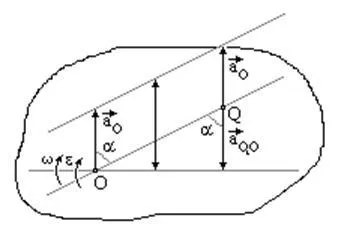
Accelerația centrul instantaneu se află pe o linie trasată la un unghi a (tga = e / w 2) la accelerarea punctului O. În acest caz, necesitatea de a amâna accelerare în direcția Ao săgeților arc unghiulare accelerare e.

Numai la punctele acestei accelerari linie dreaptă și accelerarea AO rotatiei AQO poate avea direcția opusă și același lucru în valori absolute.

Centrul de Instantanee este singurul punct cifra de accelerație, accelerarea care la un anumit moment de timp este zero. La un alt timp de accelerare centrul de față este, în general, într-un punct diferit de o figură plan.

În cazul în care poziția centrului instantaneu al accelerației este cunoscută, atunci selectarea pentru pol, pentru a accelera un punct arbitrar A avem:

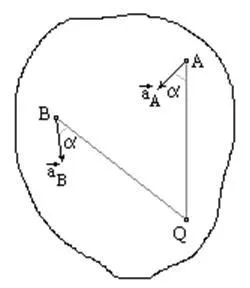
și accelerația aA îndreptate la un unghi de la AQ segment care leagă punctele A și Q în direcția săgeții e arc.

Accelerații două puncte A și B prezentate în figură, amplitudinile lor sunt egale

Subtotal: accelerarea punctelor unei figuri plane cu mișcare plan poate fi definit ca mișcarea de rotație a unei figuri plane în jurul centrului accelerațiile instantanee cu o viteză unghiulară w e și accelerația unghiulară.

Pentru a calcula viteza de presupus că cifra este rotită în jurul centrului instantaneu de viteze pentru a calcula accelerațiilor presupus că cifra se rotește în jurul centrului instantaneu de accelerare. În general, aceste centre sunt diferite puncte ale unui plan figura.

Accelerarea punctelor unei figuri plane cu mișcare plan puncte similare viteze pot fi calculate în două moduri: în conformitate cu formula care exprimă dependența de accelerare a două puncte de o figură plană (Metoda 1) și formula folosind instant accelerațiile center (metoda 2). Adesea accelerații centru de instantanee (cu excepția w sau e fiind egal cu zero) este poziționată astfel încât este dificil să se determine distanța dintre punctele considerate figura, se recomandă să se utilizeze metoda 1 prin formula de conectare cifrele de accelerație puncte.

Metode pentru găsirea accelerațiile centrali instantanee.

Accelerările toate punctele îndreptate către centrul de accelerații instantanee, deoarece acestea constau numai dintr-o componentă normală de rotație în jurul centrului instantaneu de accelerare. Dacă știi aO. apoi AQ = aA / w2.

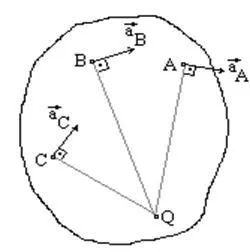
(Mișcare de translație Instantanee)

Centrul instantaneu de accelerație se află la intersecția perpendicular accelerarea punctelor. Dacă știi aO. apoi AQ = aA / e

Avem cazul general, discutate anterior. Unghiul a este reprezentată grafic de-a lungul arcului săgeții e din vectorul accelerație.

4. Să presupunem că, în acest moment de două puncte cunoscute de accelerare plan figura A și B. Luând punctul A pol, avem:

(*)

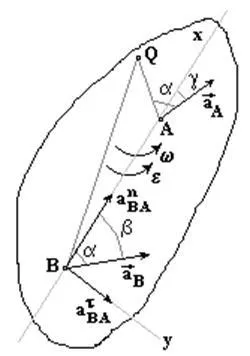
Proiectând laturile din stânga și din dreapta ale unei formule vector (x) pe axa Bx și prin obținerea

Aici, b și g, în principiu, colțuri cunoscute.

O proiecție n BA pe axa Bx luând semnul (+), deoarece este întotdeauna îndreptată spre axa de rotație (pol). atBA de proiecție. ia cu semnul (+), ceea ce sugerează că săgeata e direcționată invers acelor de ceasornic.

Proiecții ale ecuațiilor le găsim

e semn determinat după înlocuirea datelor în formulă.

Odată găsit, și e w, problema găsirii centrului instantaneu al accelerației este redusă la cazul 3.

Calculul accelerației unghiulare când mișcarea avionului.

1. Dacă știți unghiul de rotație al figurii ca o funcție de timp,

2. Găsiți viteza instantanee a centrului și, cunoscând viteza unui punct A, vom găsi viteza unghiulară de rotație a figurii w

dacă AP - Const, atunci

OA pedalier se rotește cu viteza unghiulară w e și accelerația unghiulară în jurul centrului O rulourilor r roți rază fără alunecare pe raza roții R. Să ne găsim viteza unghiulară și accelerația unghiulară de rotație al roții raza r.

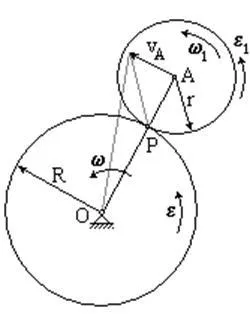
Instantanee centru viteze ale rotorului este punctul P. Apoi w1 = vA / AP = vA / r. Dar, în același punct de timp A se rotește în jurul punctului O cu viteza unghiulară w.

Când roțile dințate arc intern roată săgeata w și e roata și manivelă sunt potivopolozhnye direcție.

3. Uneori accelerația unghiulară plat figura e poate fi găsită prin proiecția pe formă axe de coordonate în direcția accelerației (de exemplu, punctul B), în cazul în care accelerația oricărui alt punct A și viteza unghiulară w forme sunt cunoscute sau pot fi calculate în avans.

Când ne folosim această formulă, și efectuarea proiecție pe axa perpendiculară aB.

manivelă OC conduce linia sirec AB, dintre care un capăt printr-un cursor este ținut în ax y, celălalt capăt A - pe axa x. Accelerarea punctului B este direcționat de-a lungul axei y. Luați în considerare proiecția formulei de mai sus pentru axa x:

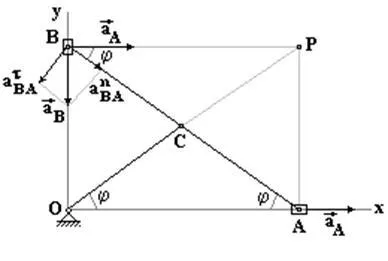
Această metodă este adecvată pentru tije de conectare, care au un punct care se mișcă într-o linie dreaptă.

Dacă accelerație cunoscute două puncte A și B în magnitudine și direcție, avem un caz 4 pentru găsirea accelerațiile instantanee centrului (proiecție formulă pentru accelerația direcția AB și perpendicular la acesta).

4. probleme în cazul în care este posibil să se determine relația identitate dintre unghiurile de rotire, transporta o diferențiere dublă. În exemplul anterior al vitezei instantanee a centrului avem.

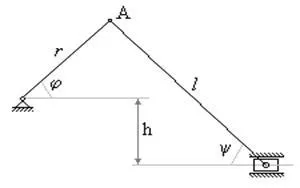
Diferențierea din nou, vom avea

Dacă dj / dt = w-const, atunci