Metoda legată Gomory

Acasă | Despre noi | feedback-ul

Problemele de programare întreg, în contrast cu lineara probleme introduse o restricție suplimentară asupra variabilelor de programare: ele pot lua numai valori întregi.

În unele aplicații, cum ar fi tipul de vehicul, această condiție este îndeplinită în mod automat în cazul în care datele sursă (numărul de bunuri expediate și primite) sunt exprimate prin numere întregi. Dar, în problema generală a tehnicilor de programare liniară soluțiile convenționale nu garantează întreg, indiferent dacă valorile de referință integrale sau fractionata.

În notație matematică problema generală a programării întreg este după cum urmează:

problemă de programare liniară economică necesită adesea o soluție întreg. Acest lucru se aplică problemelor în care variabilele indică numărul de unități indivizibile de produse, echipamente, angajații (problema de cea mai bună alocare a ordinelor de producție între întreprinderi, problema optimizării programului de producție al întreprinderilor individuale, echipamente optime și alte sarcini.). Deseori, astfel de sarcini sunt efectuate în metoda simplex de obicei, urmată de rotunjirea valorilor obținute ale variabilelor la întregi. Dar, în acest caz, este posibil să se obțină doar o aproximare a unui plan cu adevărat optim întreg.

Într-un alt grup de probleme de programare liniară sunt capacități de cantități determinabile care furnizează cel mai eficient o cerință predeterminată. Având în vedere că „transportatori“ a capacității de producție a întreprinderilor individuale act, piesă indivizibilă de echipament, și așa mai departe .. Aceste probleme sunt, de asemenea, reduse la un număr întreg de probleme de programare liniară.

De asemenea, este rațional număr întreg de tăiere problemă dimensională de material (problema deșeurilor minimizarea), deoarece acestea reprezintă variabile tind mai multe semifabricate sursă, se taie un fel sau altul.

In toate aceste sarcini soluții pot fi găsite prin metode convenționale de programare liniară, cu corectarea ulterioară și obținerea planului întreg, mai mult sau mai puțin aproape optimă. Dar există provocări, soluții de bază non-număr întreg, care nu are sens. Printre acestea se numără problema alegerii în care valorile numerice ale variabilelor sunt folosite numai pentru a determina alternativa ( „sau - sau“, „da - nu“).

Pentru modelul întreg de alegere includ unele sarcini operativ-programare, de exemplu, problema începutul secvenței optime a diferitelor produse (părți) în producție. Să presupunem necesare pentru a determina ordinea de start n părți, fiecare dintre acestea fiind procesate secvențial la mai multe mașini. variabile Hij egal cu unitatea în cazul în care partea j trebuie să fie condusă de piesă i. și zero, - în toate celelalte cazuri. Pentru fiecare j fixat. precum și pentru fiecare i. numai unul dintre n variabile poate fi egal cu una, astfel încât numărul de constrângeri ale problemei sunt următoarele:

Aceasta minimizează timpul total de prelucrare a tuturor pieselor de pe mașinile din grup. Soluție întreg al acestei probleme nu are nici un sens.

Există mai multe metode de rezolvare a problemelor de programare întreg. Cea mai cunoscută metodă de Gomory. bazat pe utilizarea metodei simplex.

Luați în considerare conceptele matematice: congruența numere întregi, un număr întreg și partea fracționară a numărului. Numărul un număr congruente b dacă și numai dacă diferența a - b este un număr întreg. Congruență denota trei linii orizontale (≡); astfel, un ≡ b. în cazul în care a - b este un număr întreg.

Toate numerele întregi sunt congruente între ele și sunt congruente cu zero. Elemente neîntreg poate fi reprezentat ca o sumă a întreg și partea fracționară a numărului a = [a] + a>. Parantezele reprezintă partea întreagă, încheiat în ele, creț - luând partea fracționară a numărului.

Proprietățile congruență numerelor:

În rezolvarea problemelor de programare întreg de primă etapă Gomori coincide cu calculul obișnuit al algoritmului simplex. Soluția rezultată va satisface, în general, toate condițiile problemei, în plus față de cerințele integralității (este posibil, desigur, pentru a obține o soluție întreg la prima etapă). În cazul în care între valorile variabilelor din planul optim (punctul A din figura 13) este fracționată, este o limitare suplimentară, ca și în cazul în care „cut-off“, partea fracționară a soluției (linia 1 din figura 13), dar lasă în loc toate constrângerile problemei, care ar trebui să îndeplinească planul optim. O limitare suplimentară este atașat la constrângerile inițiale ale problemei și a sistemului extins reaplicate procedura simplex. Dacă soluția optimă va fi din nou un non-integral (punctul B din figura 13), apoi se adaugă una restricție suplimentară (Linia 2 în figura 13), iar procesul de calcul se repetă. Algoritmul permite un număr finit de pași pentru a ajunge la soluția optimă întreg (dacă există) (punctul C din figura 13).

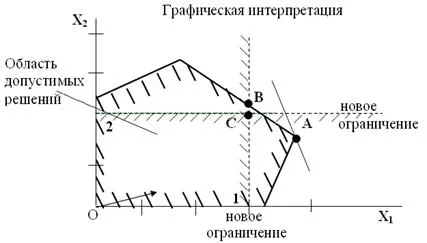
Fig. 13. Metoda reducerilor Gomory

Exemplu de rezolvare a problemelor de programare întreg. Pentru a achiziționa echipamente pentru noul site de producție de 20 de unități monetare alocate Echipamentul trebuie să fie luate pe o suprafață care nu depășește 38 m 2. Întreprinderea poate dispune de echipamente de două tipuri: mai puternic aparatul de tip O valoare de 5 den.ed care necesită zona de producție de 8 (treceri considerând) m 2 și asigură productivitate 7 mii de unități pe schimb; mașini mai puțin puternice de valoare de tip B 2 den.ed suprafață ocupă de 4 m 2 și 3 care dau o schimbare de mii de unități.

Este necesar să se calculeze varianta optimă a achiziției de echipamente care furnizează date la un maxim limitează performanța generală a site-ului.

X1 este notat cu numărul de autovehicule achiziționate prin A și x2 - numărul de mașini achiziționate B, obținem condițiile matematice ale problemei:

maximaliza 7h1 + 3x2 → max

în condiții: 5x1 + 2x2 ≤ 20

Folosirea suplimentară a inegalității variabilă x3 și x4 sursă convertită în (furnizată forma canonică):

Dacă baza variabilelor x1 și x2 - întregi, ecuația urmează direct ca variabile x3 și x4 pot lua numai valori întregi.

Problema este rezolvată inițial, fără a ține cont de cerințele integralității.

tabel Simplex este după cum urmează:

Planul optim X1 = 1, X2 = 7,5; maximă a funcției obiectiv este de 29,5. Astfel, este necesar să se cumpere un tip de mașină A și tip 7 mașină B (8 mașini nu au suficienți bani sau spațiu), apoi de ieșire de volum va fi f (x) = 7 × 1 + 3 × 7 = 28000. Unități .

Găsiți o soluție întreg de Gomory. X2 variabilă. au primit o valoare neîntreg în termeni, este următoarea ecuație, care rezultă direct din tabelul de mai sus simplex:

Această ecuație trebuie să fie în mod evident adevărată pentru o soluție număr întreg valid.

Deoarece X2 - un număr întreg, atunci întregul este expresia de pe partea dreaptă a ecuației; în consecință, amploarea pe partea dreapta a acestei ecuații este congruent cu zero:

Având în vedere proprietățile congruenta de mai sus și faptul că X3 și X4 - întregi, expresia poate fi convertită la următoarele:

Deoarece X4 - un număr întreg non-negativ, avem:

0,25X4 = 0,5 sau 1,5 sau 2,5. ;

Această inegalitate se transformă în ecuație și se adaugă la constrângerile sistemului original, care conține acum următoarele trei ecuații:

Repetând procesul de soluționare a metodei simplex aplicat unui sistem de constrângeri extinse, obținem un nou plan optim, în care valorile variabilelor incluse în baza sunt: ​​X1 = 2; X2 = 5; X4 = 2 (restul de spațiu liber).

Astfel, soluția obținută întreg optimă a problemei: performanța maximă constrângeri de date (. 29 mii de unități), cu condiția 2 cumpărare de tip A și tip B mașină 5 mașini

Filiala și legat

Această metodă poate fi aplicată pentru a rezolva ambele probleme integral și parțial întregi de programare discrete.

Să presupunem că pentru fiecare variabilă număr întreg, puteți seta limite superioare și inferioare, în care, desigur, conține valorile optime

De obicei, Hj = 0, dar acest lucru nu este obligatoriu. Problema este rezolvată prin metoda simplex. Dacă Xk presupune valori fracționare, se crede că soluția optimă a problemei, va satisface constrângerile liniare Xk ≤ dk. sau o restricție liniară Xk ≤ Dk + 1. unde Dk = [Xk] - cel mai apropiat număr întreg latura mai mică de la Xk valoare; Dk + 1 - cel mai apropiat întreg într-un mod mare de Xk. Astfel, Hj ≤ Dk ≤ Vj - 1. Apoi, este necesar pentru a rezolva o serie de probleme de programare liniară prin metoda simplex:

Obținem procesul iterativ, reprezentat ca un arbore al cărui nod corespunde soluției problemei inițiale și cele două ramuri conectate la acestea sunt soluții ale unei perechi de sarcini de programare lineară A și B. Valoarea rezultată a funcțiilor obiective în același timp, poate fi mai mică sau egală cu valoarea funcției obiectiv a problemei inițiale f ( X) A ≤ f (X) -0; f (X) B ≤ f (X) -0. Fiecare dintre cele două noi ramuri a primit nod poate avea ramificare în continuare a acesteia.

1) Un proces iterativ continuă până când se obține ramura până primit între planurile soluție întreg, valoarea funcției obiectiv trebuie să fie mai mare sau egală cu valorile funcțiilor altor scopuri de ramificare noduri.

2) Dacă la următorul pas iterație ambele au soluții întregi ai problemei, vertexul selectat sarcina cu valoare mai mare a funcției obiectiv corespunzător pentru ramificare ulterioară. Pentru una dintre variabilele care au primit valori fracționare, compilate noi restricții pentru următoarele probleme de programare liniară.

3) Dacă la următorul pas de repetare, una dintre sarcinile are o soluție întreg, iar dintre valorile variabilelor din a doua problemă, există fracționată, sunt selectate din sarcina cea mai mare valoare a funcției obiectiv. În cazul în care o sarcină a primit o soluție întreg, procesul se termină, și dacă sarcina cu valorile fractionare ale variabilelor, procesul de ramificare în continuare se realizează pentru ea.

4) Dacă nu sunteți la următorul pas iterație, unul dintre obiectivele deciziei, iar a doua problemă dintre variabile în soluția rezultată are o valoare fracționată. Apoi, pentru primul proces de ramificare sarcină este terminată, și pentru transformarea în continuare a doua sarcină este selectată una dintre variabilele non-întregi, pentru care se prezintă restricții suplimentare pentru o nouă pereche de probleme de programare liniară.

5) Dacă la următorul pas iterație una dintre problemele nu este soluția, ca și pentru cealaltă soluție întreg obținută, și există alte opțiuni cu valoare întreagă mai mare a funcției obiectiv pentru care este posibil să se continue ramificare, procesul se termină, iar soluția găsită soluția este soluția optimă întreagă a originalului sarcină.

În cazul în care sarcina selectată conduce la rupere (fundatura) sau valoarea funcției mai mică decât cea în problema V.1f (X) A.4