metoda de matura

Mai mult, prin intermediul ecuațiilor (1.7) și coeficienții progonochnyh ale expresiilor (1.8) și (1.9) sunt calculați secvențial xn-1. -Xn 2. x1.

La punerea în aplicare a metodei de baleiere este necesar să se ia în considerare faptul că, sub rezerva

sau cel puțin un bi are inegalitatea strict (1.12), distincția între „0“ se elimină, iar sistemul are o soluție unică.

Rețineți că starea (1.12) este suficientă, dar nu este necesar. În unele cazuri, sisteme bine condiționate, (1.7) metoda matura poate fi stabilă și nerespectarea condiției (1.12).

Schema algoritm metoda baleiere poate avea forma prezentată în figura 1.2.

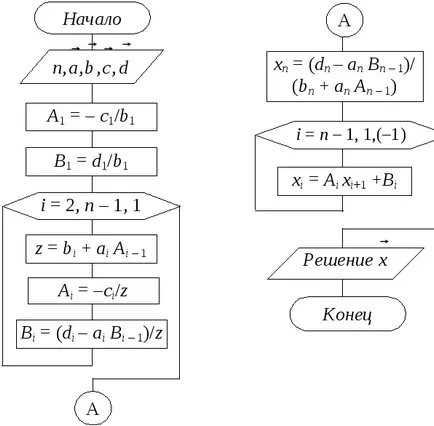
Figura 1.2 - Schema bloc a metodei matura

Metode iterative de rezolvare Slough

Avantajul metodelor iterative este aplicabilitatea lor la sistemele și sisteme de comandă de mare, samoispravlyaemost și ușor de implementat pe un computer bolnav condiționat. Metode iterative de calcul începutul postului necesită nici o aproximare inițială la soluția dorită.

Trebuie remarcat faptul că condițiile și rata de convergență a procesului iterativ depind foarte mult de proprietățile matricei sistemului A și a alegerii aproximațiilor inițiale.

Pentru a aplica metoda de iterații sistemului original trebuie să fie adus la mintea iterativ

apoi efectuați procesul iterativ prin formulele de recurență:

Matricea G și vectorul

obținut prin transformarea sistemului original.

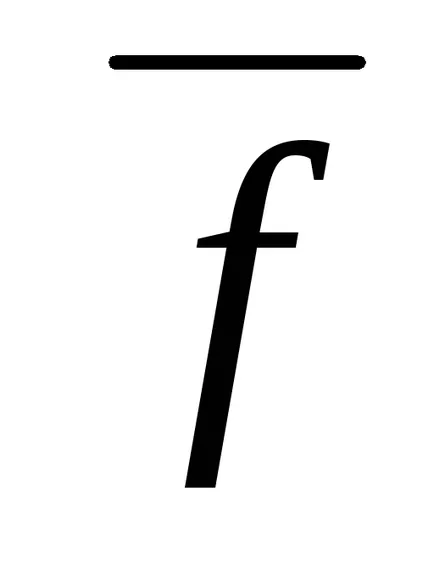
Pentru convergența metodei (1.13 *) este necesar și suficient ca | i (G) | <1, где i (G ) — все собственные значения матрицы G. Сходимость будет и в случае, если ||G || <1, ибо |i (G )| < ||G || ( — любой).

Simbolul ||. || Este norma matricei. Pentru a determina valoarea sa de multe ori opri pentru a verifica două condiții:

|| G || =

sau || G || = , (1.14)

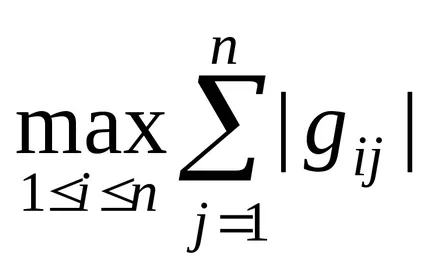
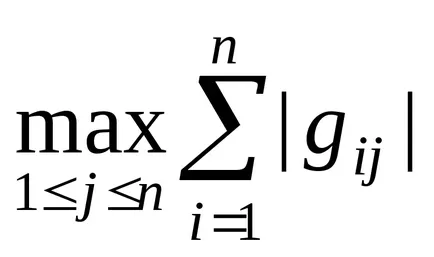
unde

. Convergența este garantat, de asemenea, în cazul în care sursa are matritsaA diagonală dominantă, adică. E.

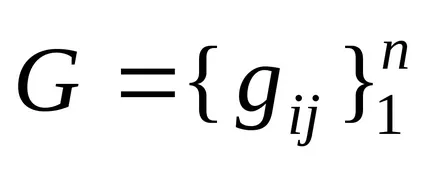
Atunci când condițiile (1.14) sau (1.15) este satisfăcută, metoda iterația converge pentru orice aproximare inițială

. Cel mai adesea, vectorsau de a lua zero sau unitate, sau vectorul în sinedin sistem (1.13).

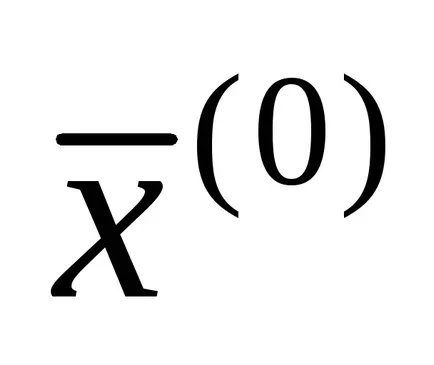
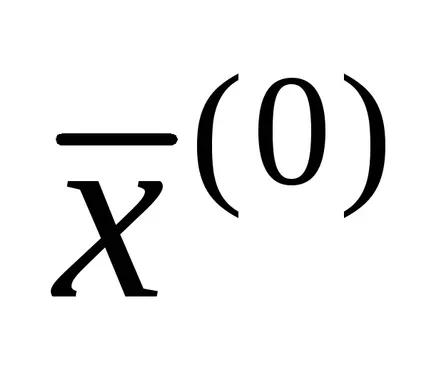
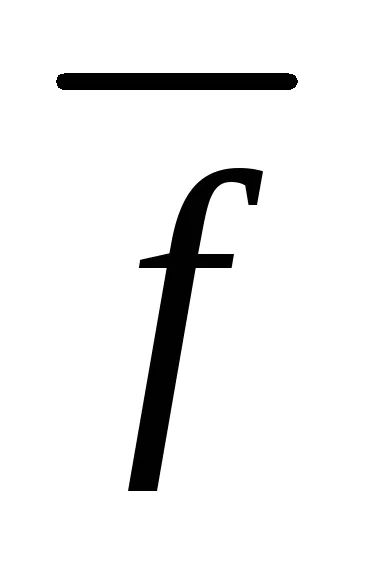
Dacă condiția (1.15), apoi conversia la forma iterativă (1.13) poate fi realizată prin simpla rezolvare fiecare i th ecuație a sistemului (1) în raport cu xi la următoarele formule de recurență:

Dacă matricea A nu este poziția dominantă pe diagonală, acesta trebuie să fie realizată prin oricare dintre transformările sale lineare care nu încalcă echivalența lor.