matrice de multiplicare
Matricea de multiplicare - este una dintre cele mai comune operații cu matrice. Matricea, care se obține după înmulțirea se numește produsul matricelor.
Produsul de AM matrice × n matrice să fie Bn x k matrice Cm x k astfel încât elementul de matrice C. situat în i-lea rând și j th coloană, adică cij element este suma produselor elementelor i -lea rând al matricei A corespunde elemente j th coloană a matricei B.
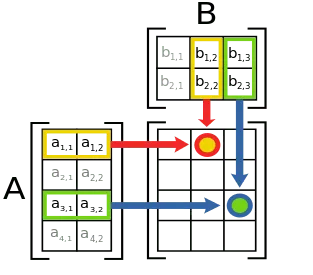
matrice de multiplicare proces este posibilă numai atunci când numărul de coloane din prima matrice este numărul de rânduri de-a doua matrice.
exemplu:
Este posibil să se înmulțească matricea matricei?
m = n. Aceasta înseamnă înmulțirea matricei de date poate fi.
Dacă matricea sunt interschimbate, apoi, cu astfel de matrici, înmulțire nu mai este posibilă.
m ≠ n. astfel, este imposibil să se efectueze multiplicarea:
Destul de des puteți găsi locuri de muncă un truc atunci când elevul este invitat să se multiplice matrici. care, evident, nu poate fi de multiplicare.
Vă rugăm să rețineți că, uneori, este posibil să se multiplice matrici și așa și așa. De exemplu, pentru matricea și MN eventual multiplicarea. și multiplicare NM.
matrice de multiplicare.
Operația de multiplicare matrice - nu este o operațiune foarte complexă. Matricea de multiplicare este mai bine înțeleasă cu exemple specifice, deoarece Numai determinare poate fi foarte confuz.
Să începem cu un exemplu foarte simplu:
Ar trebui să fie înmulțită cu. În primul rând da o formulă pentru acest caz:
- există se observă o regularitate bună.
În continuare, un exemplu mai complex:
Formula pentru acest caz :.
Matricea de multiplicare rezultat:
Rezultatul este așa-numitul matrice zero.
Este important să ne amintim că nu funcționează aici, „regula permutare plasează termenii“ ca aproape întotdeauna NM MN ≠. Prin urmare, ceea ce face operația de multiplicare matrice, în orice caz, nu poate fi interschimbate.
Acum, ia în considerare exemple de multiplicare matrice al treilea ordin:
Formula este foarte similar cu ultima:
Multiplicarea unei matrice printr-un număr.
Multiplicarea unei matrice de un număr - aceasta este aceeași matrice de multiplicare, cu excepția faptului că prim loc de-a doua matrice este luată. După cum s-ar putea ghici, această multiplicare este mult mai ușor de efectuat.
EXEMPLU Numărul matrice de multiplicare:
Aici totul este clar - de a multiplica o matrice printr-un număr. fiecare element al matricei trebuie să fie multiplicată succesiv cu un număr specificat. În acest caz - 3.
Un alt exemplu util:
- matrice de multiplicare cu un număr fracționar.
Primul pas vă va arăta ce să nu facă:
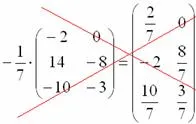
Atunci când o matrice este înmulțită cu un număr fracționar nu trebuie să facă nici o fracțiune în matrice, deoarece este în primul rând complică doar o acțiune în continuare cu matricea, și în al doilea rând, greu de verificat soluțiile profesorilor.
Și, în plus, nu este necesar să se împartă fiecare element al matricei la -7:
.
Ce ar trebui făcut în acest caz - este de a face mai puțin într-o matrice:
.
Dacă ați avut un exemplu, atunci când toate elementele matricei va fi împărțită la 7 fără reziduuri, atunci se poate (și ar trebui!) Să fie partajate.
În acest exemplu, este posibil și necesar să se multiplice toate elementele matricei pe ½, deoarece fiecare element al matricei este divizibil cu 2, fără rest.
Notă: matematici superioare conceptul de școală „diviziune“ nu este teorie. În schimb, expresia „este împărțit în“ puteți spune întotdeauna „este înmulțită cu o fracțiune.“ Aceasta este, diviziunea - acesta este un caz special de multiplicare.