mașină Turing
Una din prima definiție formală a algoritmului a fost de a determina matematicianul englez A.M.Tyuringa. În 1936 el a descris schema unei mașini abstracte constând dintr-o bandă fără sfârșit și mașina, și a sugerat de asteptare algoritm care este capabil să facă această mașină. Cu această definiție, ceva ce nu se poate face de către o mașină Turing nu este un algoritm. Calculatoarele sunt, de asemenea, concepute pentru a efectua algoritmi, dar este un dispozitiv de reală, în timp ce mașina Turing este o abstracție. Noi abstractizare membrele de memorie.
O mașină Turing constă dintr-un infinit în ambele părți ale benzii împărțit în celule și mașină. Fiecare celulă poate fi unul dintre personajele alfabetului, care sunt reprezentate în datele. În cazul în care celula este gol, atunci spunem că există un simbol gol. Alfabete pot fi diferite, dar pentru o anumită mașină Turing selectează orice alfabet. Aparatul se poate deplasa de-a lungul benzii și pe rând „observa“ conținutul celulelor. Cuvântul de intrare este plasat pe centura de o literă în celulele aranjate într-un rând și ia un număr finit de celule. Partea din stânga și din dreapta al cuvântului de intrare pe banda sunt doar celule goale. Masina este într-o stare a unei multitudini predeterminate de spoturi și o singură celulă.
mașini Turing locul de muncă de atribuire poate fi descrisă ca un program - tabel. În fiecare celulă a programului, este necesar să se specifice ce ar trebui să efectueze operații automate, dacă fiind într-o anumită stare, el „vede“ această scrisoare. În general, aparatul fiind în măsură să

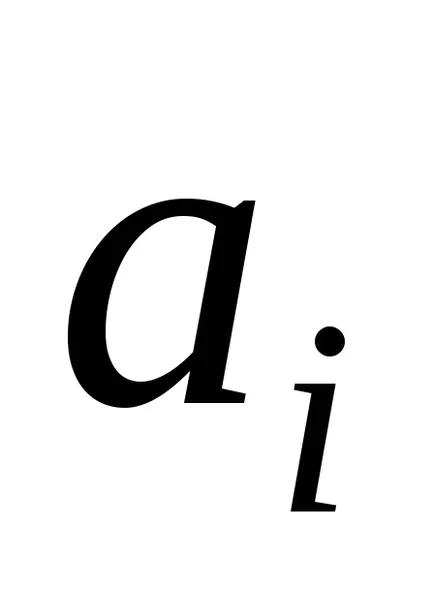
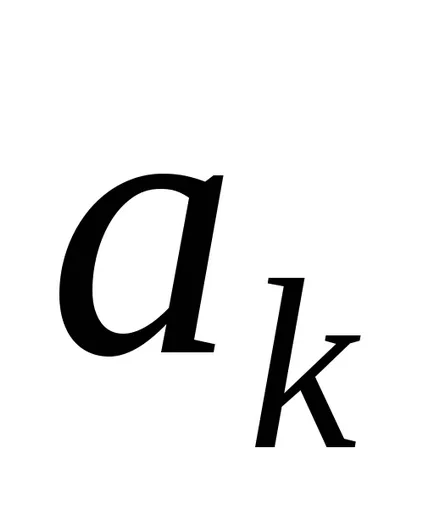


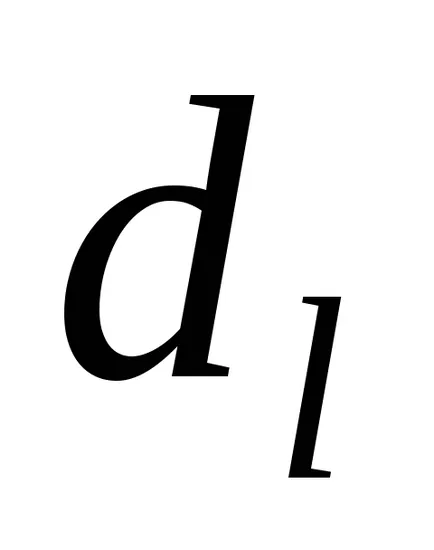
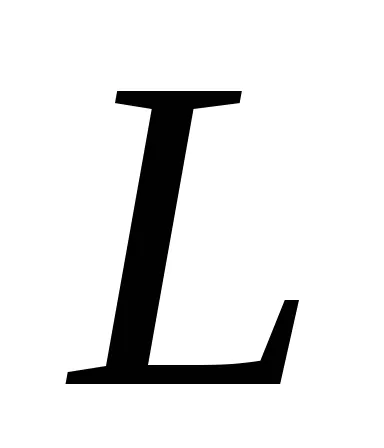
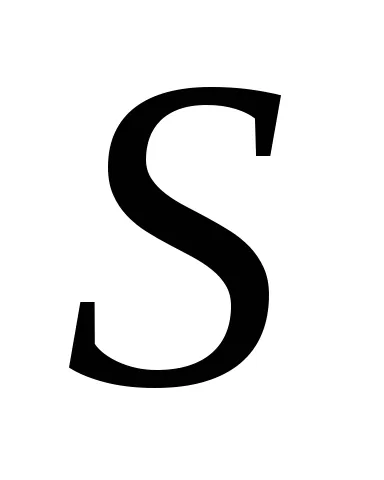

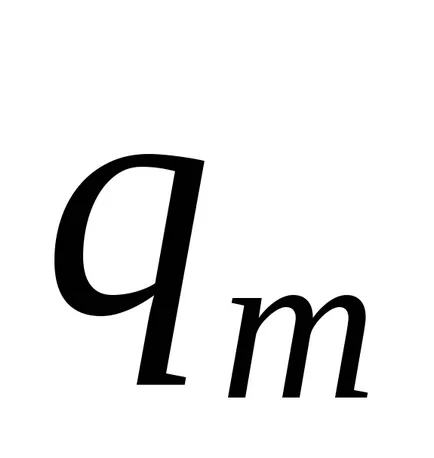
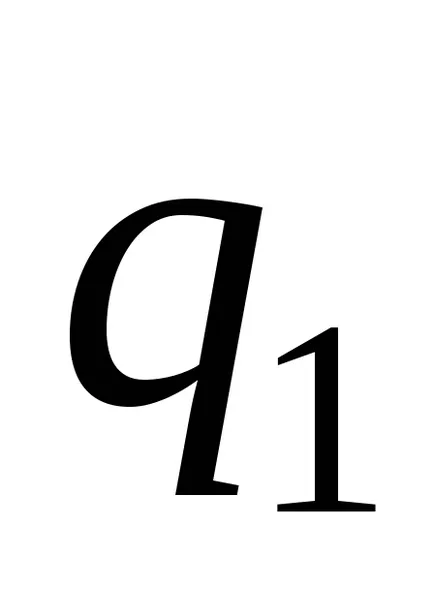
Turing Masina de configurare este un set de condiție starea internă a benzii, poziția pe mașină bandă. configurația mașinii Turing va fi scris sub forma
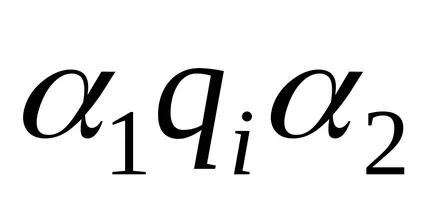
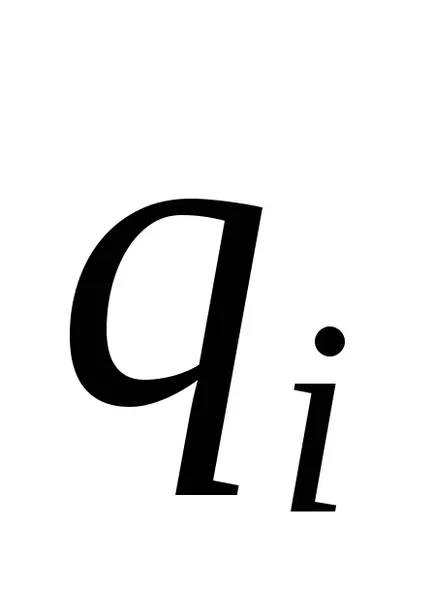

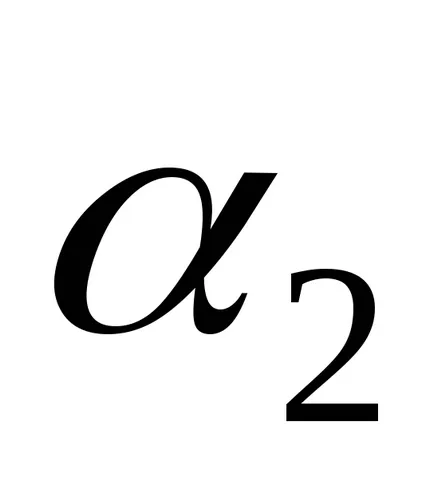
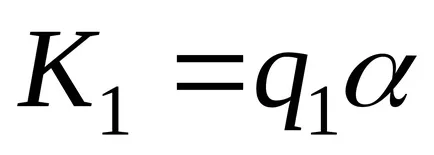
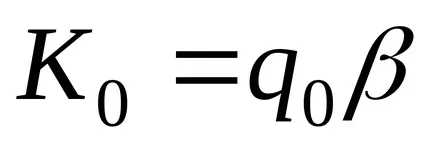
mașină Turing calculează o funcție parțială corect


dacă
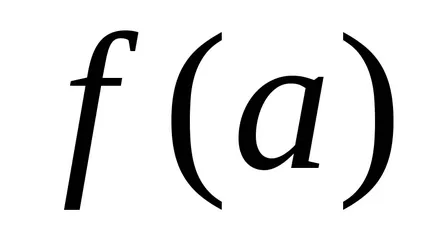
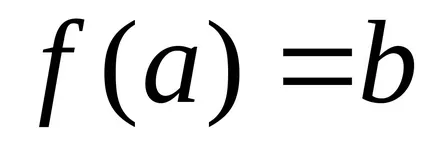
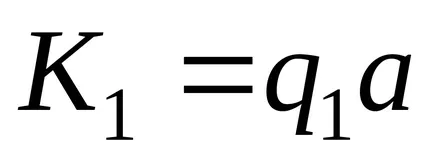
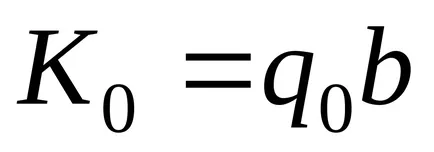
dacă
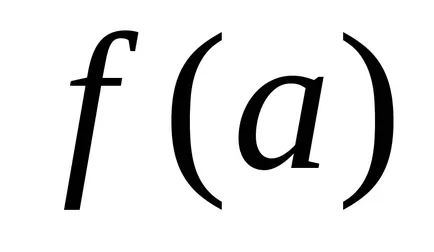
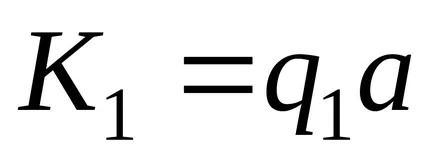
aici

funcție
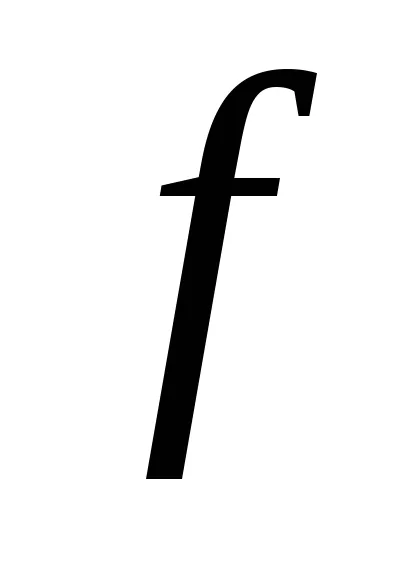
mașină EXEMPLU Turing, care transportă configurație inițială
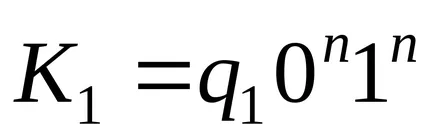
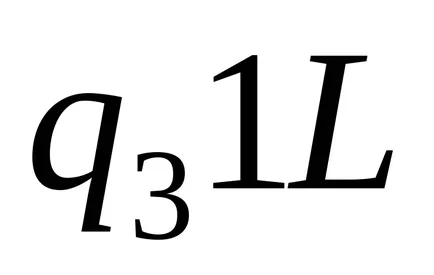
Descrierea diferitelor algoritmi pentru mașini și dovedind fezabilitatea diferitelor algoritmi compoziții, Turing a arătat convingător varietate de posibilități oferite de designul lor, ceea ce ia permis să vorbească cu următoarea teză:
Teza Turing. Fiecare algoritm poate fi pus în aplicare corespunzător mașinii.
Această teză este o definiție formală a algoritmului. Acesta vă permite să dovedească existența sau absența unor algoritmi, care descrie mașina Turing corespunzătoare sau dovedește imposibilitatea de a construi ei. nu poate fi dovedită teza Turing, deoarece modul său de redactare nu definește noțiunea de „orice algoritm“, adică, în partea stângă a identității. Ea poate fi justificată numai prin prezentarea o varietate de algoritmi bine cunoscute sub formă de mașini Turing. Sprijinul suplimentar al acestei teze constă în faptul că acesta a fost sugerat mai târziu câteva definiții comune ale conceptelor de algoritm și de fiecare dată a reușit să demonstreze că, deși noile scheme algoritmice și un aspect diferit, ele sunt de fapt echivalente cu mașinile Turing: tot ceea ce este realizabilă într-una dintre aceste modele, se poate face în cealaltă. Aceste afirmații sunt dovedite strict, deoarece acestea sunt deja vorbesc despre identitatea schemelor formale.
Markov algoritm normale
În 1954, matematicianul sovietic AA Markov a propus un sistem de algoritmică diferit echivalent cu o mașină Turing, în care datele sunt convertite bazate pe alte principii. In schema algoritmică Markov are nici un concept de bandă, și necesită acces direct la diferite părți ale cuvintelor convertite. Markov numit schema algoritmică a algoritmului normal. Conceptul unui algoritm normale are multe avantaje atât natura fundamentală și metodică, sa dovedit a fi fructuoasă și convenabil. Pentru a rezista testului timpului și a dovedit viabilitatea, acesta - împreună cu conceptele de funcții recursive și mașini Turing - ferm stabilit în utilizarea științifică a teoriei moderne a algoritmilor.
Algoritmul normal Markov este un set ordonat de permutări (produs) de forma
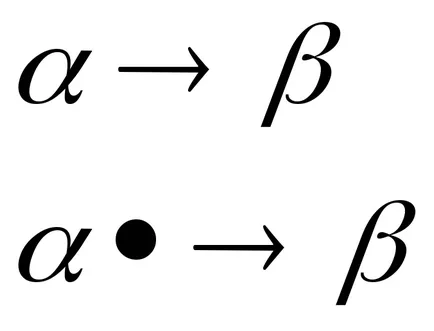
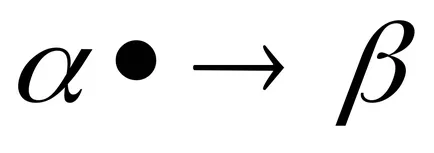
Formula de substituție este utilizat pentru a înlocui subwords într-un cuvânt de transformare. Și subwords substituent înlocuibil în formula sunt separate prin una dintre săgețile sau → • →. tipul de produse

Ca un exemplu algoritm pentru a calcula funcția în alfabetul
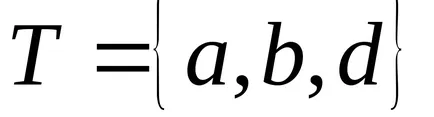

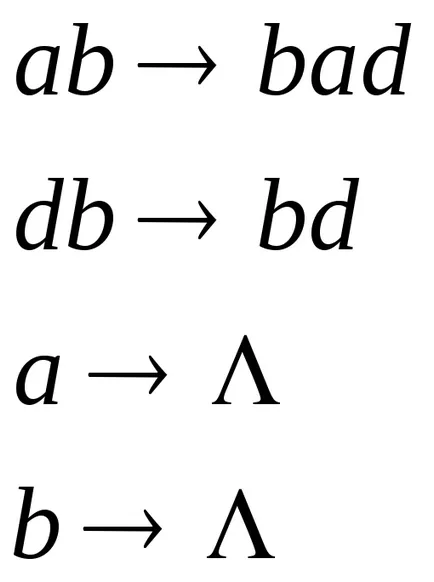
Efectuarea algoritm Markov este împărțit în etape. Fiecare pas include găsirea unui ordin primă formulă de substituție aplicabilă transformarea cuvânt și executarea corespunzătoare acestei formule este înlocuită. Dacă încercați să aplicați formula de substituție este că există mai multe apariții ale părților sale pot fi înlocuite, înlocuiește întotdeauna prima (stânga) apariția. Procesul algoritmului se termină în două cazuri:
- fie toate formulele erau inaplicabile,
- sau formula finală, în care stânga și săgeată dreapta → parts subword a fost aplicată în ultima etapă.
În oricare dintre aceste cazuri, se crede că algoritmul normală este aplicabil un cuvânt de intrare dat.
Dacă în timpul executării unui număr infinit de ori a algoritmului sunt substituții simple ale formulei utilizate, algoritmul nu este aplicabil dat cuvântul de intrare.
Algoritmul normal este numit un algoritm normal de peste alfabetul
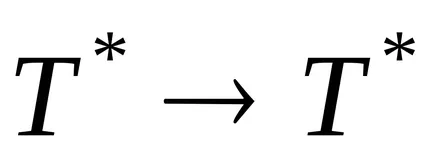

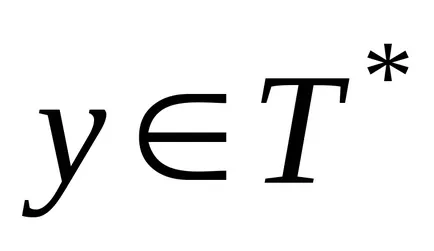
algoritm normale

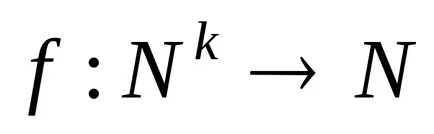

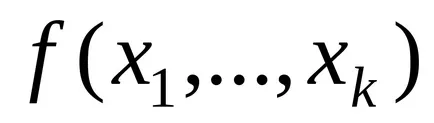
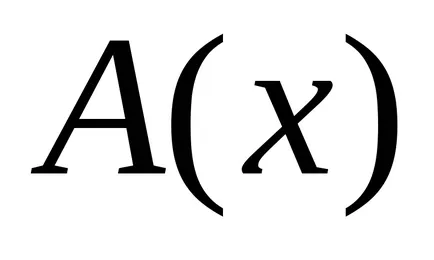
Algoritmică Markov Turing circuit și sunt echivalente în sensul că toți algoritmii descriși în unul dintre ele poate fi descrisă în alta. Aceste circuite nu pot fi realizate fizic, deoarece acestea sunt o abstracție matematică ce permite un număr nelimitat de cuvinte lungime mai mare care apar în procesul de transformare.