Laplace Teorema locală și integrală
Este necesar să se calculeze: a) așteptarea M (X), b) dispersia D (X), c) standardul sigma deviație.
Decizie. a) speranța matematică M (X) a unei variabile aleatoare X discretă este suma produselor tuturor valorilor pereche posibile ale variabilei aleatoare corespunzătoare probabilității de valori posibile. În cazul în care X este o variabilă aleatoare discretă definită folosind un tabel (1), atunci așteptarea M (X) se calculează cu formula:
Așteptarea M (X) este numită și valoarea medie a variabilei aleatoare X. Folosind (2), obținem:
b) Dacă M (X) este speranța matematică a unei variabile aleatoare X, diferența X-M (X) este deviația variabila aleatoare X este media. Această diferență caracterizează dispersia variabilei aleatoare.
Dispersia (împrăștiere) a unei variabile aleatoare discrete X este speranța matematică (valoarea medie), o deviere pătrată a variabilei aleatoare din așteptările sale. Astfel, prin definiție, avem:
Noi calcula toate valorile posibile ale abaterilor la pătrat.
Pentru a calcula varianța D (X), formează abaterea pătrat drept de distribuție și apoi se aplică formula (2).
Acum vom găsi speranța matematică M (X 2).
M (X 2) = (48) 2 ∙ 0,2 + (53) 2 ∙ 0,4 + (57) 2 ∙ 0,3 + (61) 2 ∙ 0,1 =
Aplicarea (4), obținem:
D (X) = 2931,2- (54) 2 = 2931,2-2916 = 15,2.
După cum vedeți, avem același rezultat.
c) Varianța dimensiune este pătratul dimensiunii variabile aleatoare. Prin urmare, pentru caracteristicile de împrăștiere a valorilor posibile ale variabilei aleatoare în jurul valorii sale medii mai convenabil să ia în considerare mărimea care este egală cu valoarea aritmetică a rădăcinii pătrate a varianței, adică
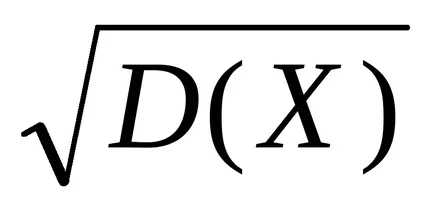
Aplicarea (5), avem: σ =
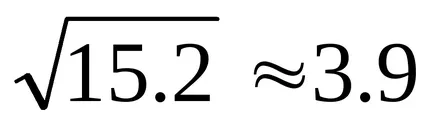
Exemplu. Aleatoare X variabila are o distribuție normală. Așteptarea M (X) = 5; dispersiyaD (X) = 0,64. Găsiți probabilitatea ca un rezultat de test va avea valoarea x în intervalul (4, 7).
Decizie. Este cunoscut faptul că, dacă variabila aleatoare X este setat funktsieyf diferențială (x), probabilitatea ca X presupune valoarea aparținând intervalului (α, β), calculat prin formula
Dacă valoarea X are o distribuție normală, funcția diferențială
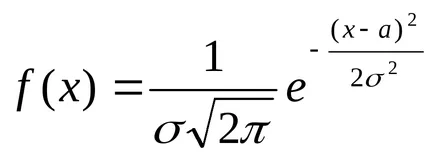
unde a = M (X) și σ =
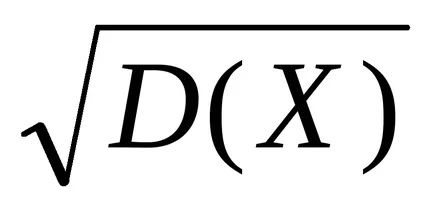
Formula (2) poate fi transformat cu ajutorul funcției Laplace.
Asigurați schimbarea. lăsa
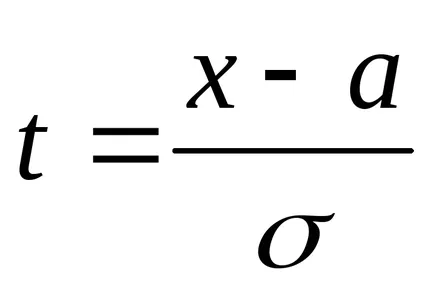
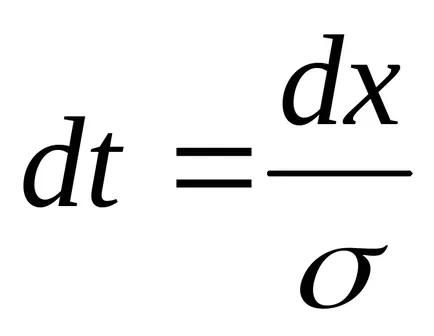
În consecință, IT2 gdet1 limite adecvate pentru peremennoyt.
Reducerea pe σ, avem
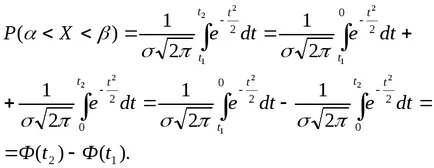
Substituția impus
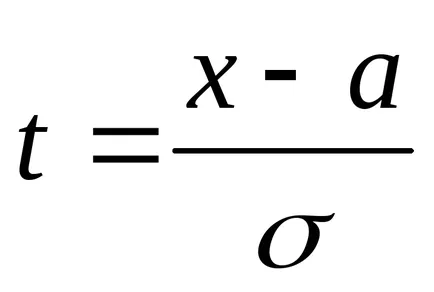
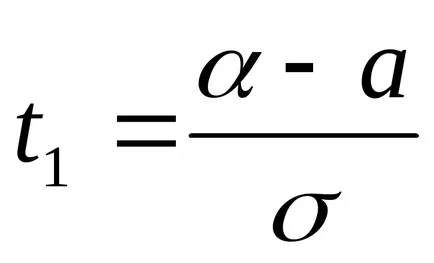
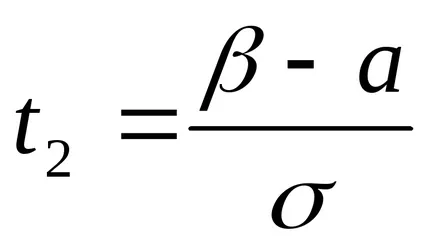
Prin ipoteză avem o problemă: a = 5; σ =
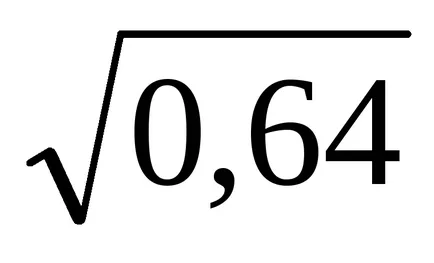
Exemplu. Se crede că lungimea abaterii de la standardul de piese produse este o variabilă aleatoare normal distribuită. Lungimea standard (așteptare) a = 40 cm, abaterea standard σ = 0,4 cm. Gaseste probabilitatea ca abaterea de la lungimea standard va fi valoarea absolută nu mai mare de 0,6 cm.
Decizie. Dacă X - lungimea elementelor, atunci starea problemei, această valoare trebuie să fie în intervalul (a-δ, a + δ), unde a = 40 și δ = 0,6.
Punerea în formula (3) α = a-δ și β = a + δ, obținem
Substituind în (4) datele disponibile, obținem:
Prin urmare, probabilitatea ca obiectele fabricate de lungime va fi în intervalul de la 39,4 la 40,6 cm este 0.8664.
Exemplu. Diametrul pieselor fabricate de plante, este o variabilă aleatoare distribuită în mod normal. Diametraa lungime standard = 2,5 cm, deviația standard σ = 0,01. În termen ce limite poti garanta lungimea diametrul părții, luată drept un eveniment semnificativ, dintre care probabilitatea este egală cu 0.9973?
Decizie. Prin ipoteză avem o problemă:
Aplicând formula (4), obținem:
Conform tabelului 2, se constată că o astfel de valoare a funcției Laplace are x = 3. Prin urmare,
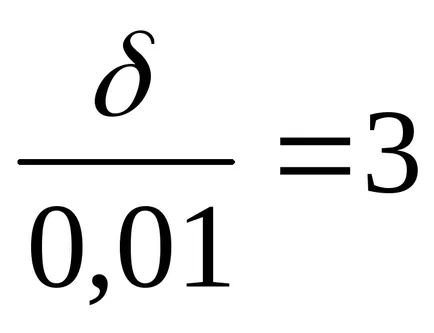
Astfel, putem garanta că lungimea diametrului va varia 2.47-2.53 cm.