Funcțiile de transfer ale sistemelor deschise și închise - studopediya

Funcția de transfer a buclei deschise (Figura 7.1.):

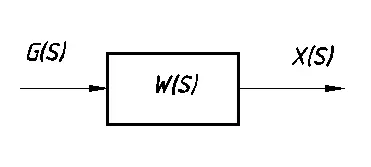
Notă: Unitatea se numește integrare, dacă numitorul este o grupare S pur; dacă S în formă pură este în numărător, legătura se numește un diferențiator.

Sistemul de ecuații diferențiale în formă de L:

Funcția de transfer a sistemului în unități de racordare a seriei (a se vedea figura 7.2 ..):

Funcția de transfer a sistemului în unități de conectare în paralel (a se vedea figura 7.3 ..):

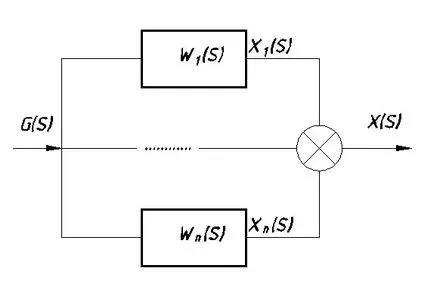
Feedback-ul local:

Sistemul ecuații cu feedback-ul (vezi Figura 7.4 ..):

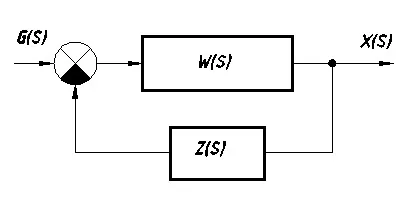
Atunci când unitatea de feedback:

Notă: în continuare W (S) este funcția de transfer a buclei deschise, F (S) este funcția de transfer a sistemului închis. Funcția de transfer a unui sistem închis:

Polinomul caracteristic al unui sistem închis:

Ecuația caracteristică a sistemului închis:

Ecuația caracteristică a sistemului deschis:

Funcția de transfer a perturbației prin:

Să considerăm sistemul prezentat în Fig. 7.5.

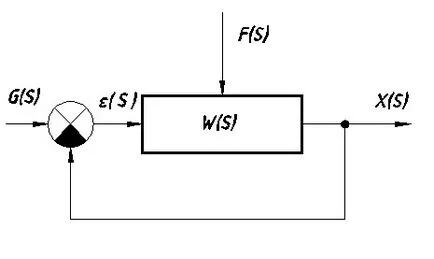
· # 949; (t) / # 949; (S) -eroare

Funcția de transfer a erorii:

Transformarea schema inițială cu normele de reforme structurale (a se vedea figura 7.6 ..):

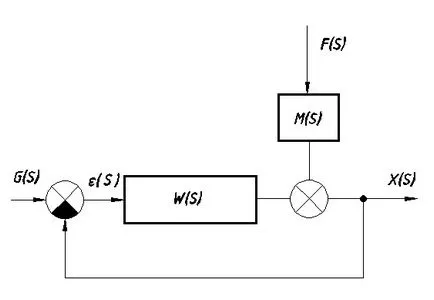
Prin urmare, funcția de transfer a perturbației prin este:

Notă: Ordinea sistemului deschis este determinată de ordinul unui sistem închis.

Ecuațiile de bază ale sistemelor de urmărire.

Ecuația diferențială a sistemului (vezi Ris.7.6.):

Ecuația diferențială a unui sistem închis:

Ecuația diferențială pentru deviația erorii:

Sistemul de ecuații diferențiale în formă de Cauchy și fără a perturba acțiunile de intrare:

Această ecuație determină mișcarea corespunzătoare a sistemului

Ecuația caracteristică pentru controlul:

. unde E - matricea identitate