Funcția de proporționalitate inversă algebra

Funcția de proporționalitate inversă - o funcție definită prin formula

unde x - variabilă independentă, k - un alt număr decât zero.

Graficul de proporționalitate inversă este o hiperbolă. Hiperbola este format din două ramuri. (Așa-numitele două din grafic).

câteva puncte pe care trebuie să știți pentru construirea hiperbolă (mai multe puncte - programul exact). Este mai bine de a alege cele x, care este convenabil de a diviza k.

Proprietățile funcțiilor inverse

1) Domeniul de determinare inversă constă din toate valorile lui x, cu excepția punctului zero:

2) Domeniul valorilor inverse - toate valorile y, altele decât zero:

3) Funcția de proporționalitate inversă nu are zerouri.

ramură hiperbolă este situată în coordonate trimestrele I și III:

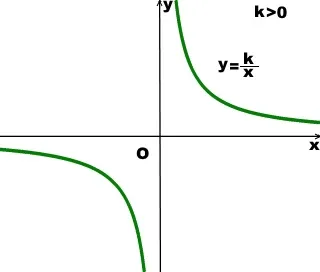
Scăderi invers proporțională cu fiecare domeniu intervale de timp, adică atunci când x∈ (-∞; 0) U (0; ∞).

Funcția are o valoare pozitivă atunci când x> 0, sau

Funcția are o valoare negativă pentru x<0, или

ramură hiperbolă situate VO II și IV coordonate sferturi:

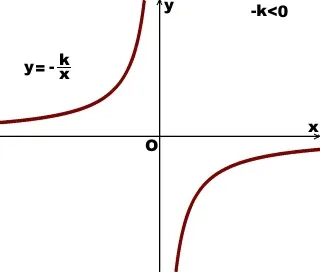
Feedback creșteri proporționale în fiecare dintre perioadele de domeniu, adică sub x∈ (-∞; 0) U (0; ∞).

Funcția are o valoare pozitivă atunci când x<0, или

Funcția are o valoare negativă când x> 0, sau

Ox și Oy este axa asimptota de invers - direct la care ramuri ale hiperbola se apropie pe termen nelimitat (dar niciodată atins).

Data viitoare te uiti la exemple concrete de modul de a construi un grafic de proporționalitate inversă.