Faza a oscilației

Introducem o altă cantitate care caracterizează oscilații armonice, - oscilațiilor de fază.

La o anumită amplitudine a oscilațiilor corpului oscilant coordonatele în orice moment în timp este determinată în mod unic prin cosinusul sau argument sine: φ = ω0 t.

Cantitatea cp, stând sub semnul funcțiilor cosinus sau sinusoidale, numita fază de oscilație. descrisă de această funcție. Faza exprimată în unități unghiulare - radiani.

Faza determină nu numai valoarea de coordonate, dar valoarea altor mărimi fizice, cum ar fi viteza și accelerația, schimbându-și armonic. Prin urmare, putem spune că faza definește la o anumită amplitudine a stării de vibrație a sistemului la un moment dat. Acesta este sensul faza de concept.

Oscilații cu amplitudini egale și frecvențele pot varia în faze.

Raportul arată cât de multe perioade au trecut de la începutul oscilație. Orice valoare a timpului t, exprimat în numărul de perioade T corespunde valorii cp fază, exprimată în radiani. Astfel, după scurgerea timpului (o perioadă sfert) după o perioadă de jumătate = π cp, după întreaga perioadă și cp = 2π t. D.

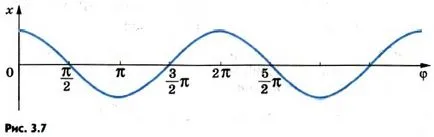
Acesta poate fi reprezentat pe diagrama de coordonate dependența punctului oscilant nu pe timpul și faza. Figura 3.7 arată același val cosinus, ca în figura 3.6, dar în loc de axa orizontală reprezintă timpul, valori diferite ale φ faze.

Introducerea de oscilații armonice folosind un sinus și cosinus. Știți deja că vibrațiile armonice ale corpului de coordonate se modifică în timp, conform legii cosinusul sau sinus. După introducerea faza de concept a discuta acest lucru mai detaliat.

Argumentul cosinus Sinus diferă de deplasare pe, ceea ce corespunde, așa cum se poate observa din ecuația (3.21), un interval de timp egal cu o perioadă sfert:

De aceea, în loc de formula x = Xm cos ω0 formula t poate fi utilizat pentru a descrie oscilații armonice

Dar această fază inițială. t. e. valoarea fazei la momentul t = 0 nu este egal cu zero.

În mod normal, vibrațiile corpului atașat la un arc sau pendul ne excita, aducând corpul pendul din poziția sa de echilibru și apoi eliberându-l. Deplasarea din poziția de echilibru posibil în momentul inițial. Prin urmare, pentru a descrie oscilații mai convenabil de a folosi formula (3.14), prin utilizarea de cosinus decât formula (3.23), cu utilizarea sinusurilor.

Dar dacă ne excita oscilații ale unui corp în repaus stimulare pe termen scurt, corpul coordonate la momentul inițial ar fi zero, și să coordoneze schimbările în timp, ar fi mai ușor să se descrie prin intermediul t sinus. E. Formula

deoarece în acest caz faza inițială este zero.

Dacă timpul inițial (la t - 0), oscilația de fază este φ, atunci ecuația de oscilație poate fi scrisă ca

schimbare de fază. Oscilațiile descrise de (3.23) și (3.24) diferă unul de altul numai în fază. Diferența de fază, sau, după cum se spune adesea, trecerea de faza oscilațiilor este. Figura 3.8 prezintă graficele coordonatei de timp pentru două oscilații armonice deplasate în fază. Figura 1 corespunde vibrațiilor comite sinuos: Xm = x păcat ω0 t, și Figura 2 - oscilații efectuate de legea cosinus:

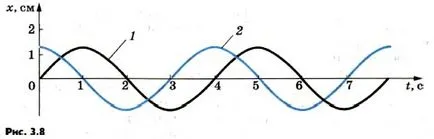
Pentru a determina diferența de fază dintre cele două oscilații trebuie oscilante magnitudine în ambele cazuri, exprimat în termeni de aceeași funcție trigonometrice - sinusul sau cosinusul.

Întrebări la alineatul

1. Ceea ce se numește oscilații armonice?

2. Cum sunt accelerarea și coordonarea cu vibrațiile armonice?

3. Cum sunt frecvența de oscilație ciclică și perioada de oscilații?

4. De ce este frecvența de oscilații ale corpului, atașat la un arc depinde de masa sa, iar frecvența de oscilație a unui pendul simplu este independentă de masa?

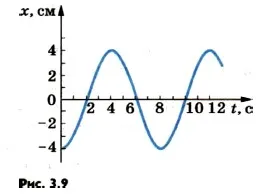
5. Care sunt amplitudinile și perioadele de trei oscilații armonice diferite, ale căror grafice sunt prezentate în figurile 3.8 și 3.9?