Curs 2 imparțiale, și coerente estimări ale parametrilor de distribuție eficiente
Pentru a obține estimări statistice o bună aproximare a parametrilor estimați, acestea ar trebui să fie imparțiale și eficiente bogat.
numita evaluare statistică impartiale


Se numește evaluare statistică deplasat


Efectiv numit evaluare statistică


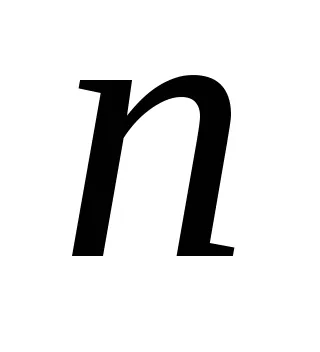
numita evaluare statistică înstărit


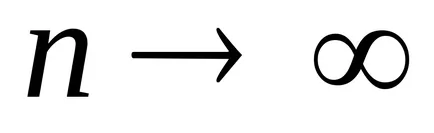
Pentru probele de dimensiuni diferite se obțin diferite valori ale mediei aritmetice și dispersiei statistice. Prin urmare, media statistică și varianța sunt valori aleatoare, pentru care există așteptări și varianța.
Calculăm așteptarea și varianța mediei aritmetice. Vom nota cu

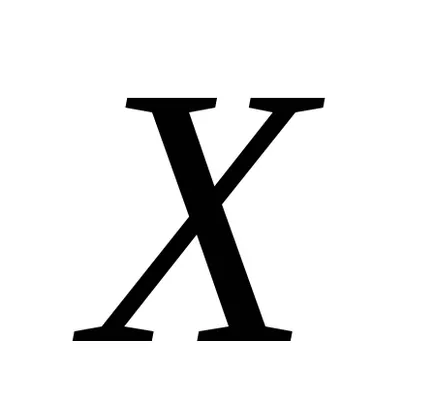
Aici, ca variabile aleatoare sunt luate în considerare:
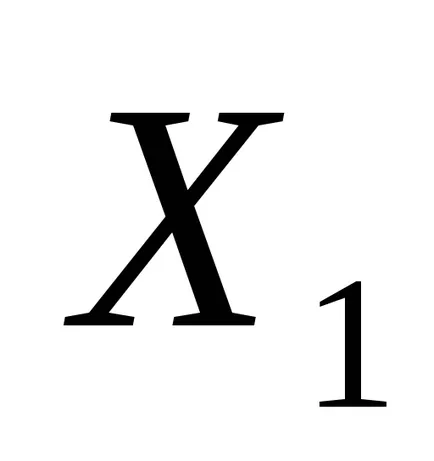

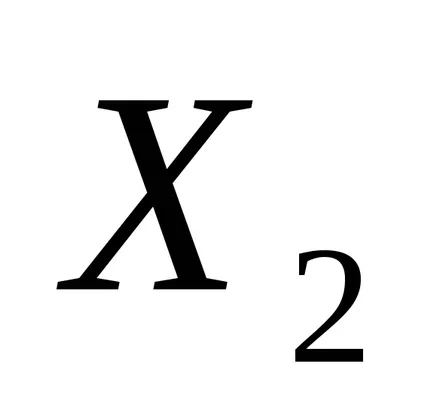
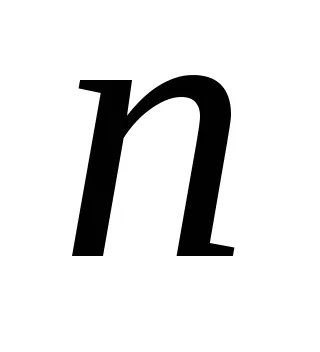


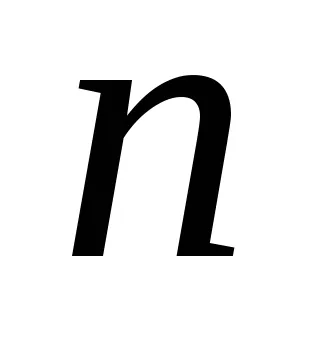
.
De la formula (1) că media aritmetică este o estimare imparțială a așteptărilor, deoarece speranța matematică este egală cu media aritmetică a speranța matematică a unei variabile aleatoare. Această estimare este, de asemenea, consecvent. Eficacitatea acestei estimări depinde de tipul de distribuție variabilă aleatoare
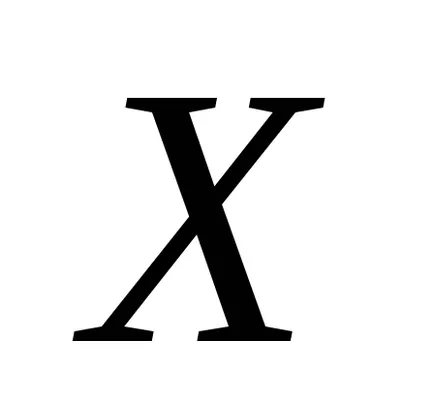
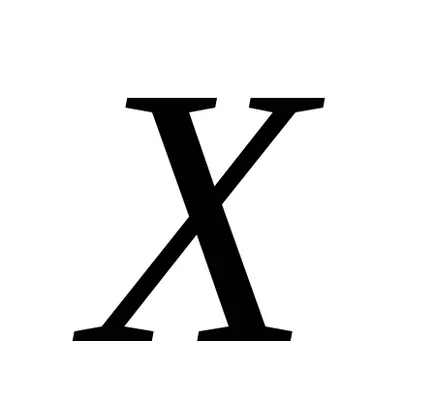
Acum vom găsi evaluarea statistică a dispersiei.
Expresia pentru dispersia statistică poate fi transformată după cum urmează:
Acum ne găsim speranța de dispersie statistică
De la Formula (6) arată că dispersia statistică anticipată diferă cu un factor de dispersie, adică Este o estimare părtinitoare a varianței populației. Acest lucru se datorează faptului că în loc de valoarea reală
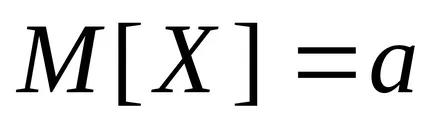

Prin urmare, vom introduce o variație statistică revizuită
Apoi așteptarea unei variații statistice revizuite egal
și anume este corectată variație statistică estimare imparțială a varianței populației. Estimarea rezultată este de asemenea consecventă.