Cilindric Nivelul de lichid vas ajunge la ce înălțime va rămâne nivel

În vasul cilindric, nivelul lichidului ajunge la 16 cm. La ce înălțime va fi în nivelul de lichid, dacă ei se toarnă în al doilea vas cilindric al cărui diametru este de 2 ori mai mare decât primul diametru? Răspunsul este exprimat în centimetri.

volumul cilindrului V = πR 2 ore.

În primul caz, volumul de lichid egal cu V = 16πR 2.

Dacă diametrul celui de al doilea vas de 2 ori mai mare decât diametrul primului vas, iar raza doilea vas de 2 ori mai mare decât raza primei nave. Prin urmare, după ce lichidul Transfuzia în al doilea vas, volumul său poate fi calculat prin formula:

V = π (2R) 2 h = 4πR 2 h, unde h - înălțimea dorită.

Deoarece volumul de lichid rămâne constantă transfuzie, aceste valori sunt:

16πR 2 = 4πR 2 h,

Cilindri și conuri au o bază comună și înălțimea totală. Se calculează volumul pistonului când volumul conului este egal cu 20.

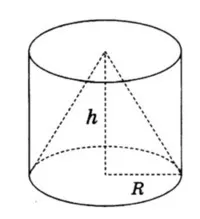
înălțimea conului egală cu înălțimea raza cilindrului și con egală cu raza cilindrului (vezi. fig.).

Volumul conului este egal cu vk = (1/3) πR 2 h = 20.

Volumul cilindrului este Vts = πR 2 3Vk = h = 3 * 20 = 60.

Prin urmare, volumul cilindrului este de 3 ori mai mare decât volumul conului și este egală cu 60.

Cilindri și conuri au o bază comună și înălțimea totală. Se calculează volumul pistonului când volumul conului este egală cu 19.

înălțimea conului egală cu înălțimea raza cilindrului și con egală cu raza cilindrului (vezi. fig.).

Volumul conului este egal cu vk = (1/3) πR 2 h = 19.

Volumul cilindrului este Vts = πR 2 3Vk = h = 3 * 19 = 57.

Prin urmare, volumul cilindrului este de 3 ori mai mare decât volumul conului și este egală cu 57.

În mod regulat înălțimea piramidei patrulater este egal cu 2, muchia laterală este 4. Găsiți volumul său.

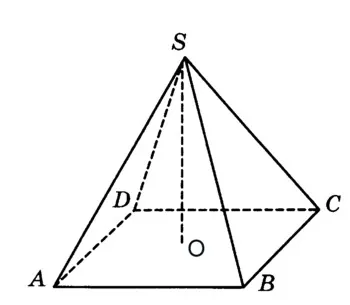
Volumul piramidei este egal cu V = (1/3) H. Sosn

Pentru H = SO = 2 condiție, SC = 4.

Baza piramidei regulate patrulateră este un pătrat. Ne găsim drumul, și anume găsi AB.

SOC unui triunghi dreptunghic de teorema lui Pitagora, avem:

SC 2 = SO 2 + 2 OC

OC 2 = SC 2 - SO 2,

OC 2 2 = 4 - 2 = 2 12,

OC = √ (12) = 2√3,

AC = 4√3, AC 2 = 48.

Din triunghiul dreptunghic ABC (dat fiind faptul că AB = BC) de teorema lui Pitagora, avem:

2 AC = AB + BC 2 2 = 2AB 2

48 = 2AB 2. AB 2 = 24.

V = (1/3) * 24 * 2 = 16.

Cilindri și conuri au o bază comună și înălțimea totală. Se calculează volumul pistonului când volumul conului este egal cu 12.

înălțimea conului egală cu înălțimea raza cilindrului și con egală cu raza cilindrului (vezi. fig.).

Volumul conului este egal cu vk = (1/3) πR 2 h = 12.

Volumul cilindrului este Vts = πR 2 3Vk = h = 3 * 12 = 36.

Prin urmare, volumul cilindrului este de 3 ori mai mare decât volumul conului și este egală cu 36.