Când d Lachh
Elevii trebuie să știe:
Logaritnica sistem de coordonate;
Procedura de construcție a caracteristicilor amplitudine-frecvență logaritmice ale unităților tipice ACS;
Procedeul de construire a caracteristicilor de fază logaritmică unități tipice ACS;
Procedura de determinare a inventarului fazei și amplitudinii folosind caracteristicile logaritmice ale unităților tipice ACS.
Material de instruire coordonate logaritmice
Construcția de sistem de APC privind caracteristicile unităților sale componente pot fi simplificate, dacă vom folosi scara logaritmică. sistem în care axele sunt depozitate în locul valorilor și logaritmului lor Logarifmicheskaya- de coordonate. Dacă există o funcție de frecvență a formei:, este logaritmul acestei expresii obținem (1)
(1) definește o APC logaritmică, a cărui parte reală este egală cu logaritmul modulului funcției de frecvență și partea imaginară - argumentul funcției de frecvență. Această caracteristică poate fi reprezentată prin două caracteristici independente LACHH și APFC.
răspuns de fază logaritmică determină modificarea în jurnalul modulului funcției de frecvență cu frecvență. Logaritmul modulului reprezentate grafic pe axa y și log frecvență pe axa x.
pentru că Expresia (1)
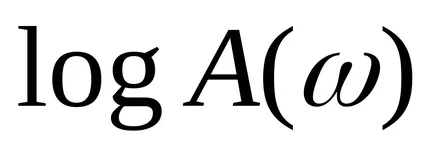
Bell este prea mare, astfel încât valoarea
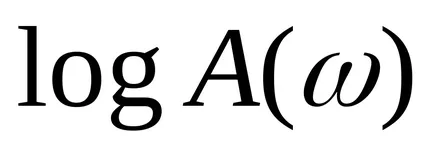
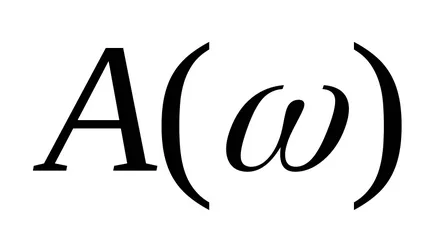
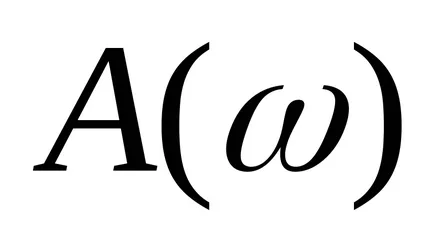
Pentru a determina logaritmii frecvențelor utilizate în unitățile acustice utilizate: octavă și deceniu.
Intervalul de frecvență între valorile deținuților arbitrare - Octave

Deceniul - intervalul de frecvență cuprinse între valoarea arbitrară


logaritmică caracteristică fazei de frecvență a unei determină schimbarea de fază în grade cu frecvență. Faza magnitudine în grade este reprezentată pe axa ordonată și frecvența schimbării -după abscisa în scară logaritmică.

Pentru un număr de real, ACS există o relație unică între caracteristica de fază-frecvență logaritmică a iadului și caracteristica amplitudine-frecventa logaritmică a iadului. Astfel de sisteme sunt numite minim faze, deoarece LFCHH LACHH predeterminate corespunzătoare, are cea mai mică valoare de fază. LACHH și LFCHH combinate, de obicei, în același grafic cu totalul abscisă.
Avantajele utilizării caracteristicilor de frecvență logaritmice
1. Vizibilitatea cursei caracteristică a imaginii în gama de înaltă frecvență, astfel cum schimbare de zece ori în frecvență corespunde schimbării de frecvență logaritmului doar 1.
2. Caracteristicile unităților de referință tipice au o formă simplă și cu precizie ridicată sunt aproximate prin segmente de dreaptă (asymptotes) având diferite înclinații. Pantele acestor segmente sunt de obicei exprimate în [dB / decadă].
3. Pentru a construi caracteristicile logaritmice ale expresiilor simple sunt folosite, deoarece ca urmare a logaritmarea lucrărilor modulului de funcții de frecvență și de ramură privată înlocuiește Sumy și diferențe.
4. Caracteristici ale sistemelor complicate pot fi preparate prin însumarea caracteristicilor tipice ale unităților lor constitutive.
5. Abilitatea de a evalua calitatea ATS, precum și răspunsul sistemului la o modificare a structurii sale.
Dă definirea coordonatelor logaritmice.
Care este amplitudinea măsurată în coordonate logaritmice.
Ceea ce se măsoară prin frecvența în coordonate logaritmice.
Așa cum este posibil să se obțină caracteristicile sistemelor complexe, cunoscând caracteristicile unităților tipice logaritmice.
Ce pantă câștig standard, în coordonate logaritmice, caracterizat prin unități tipice automate.
Referințe pe tema prelegerii: