Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare

Lăsați curba L este definită în coordonate polare:

= =

= =

=

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
.

Lungimea arcului curbei în coordonate polare sistem L =.

Exemplu: Calculați lungimea cardioidă. Prin simetrie se calculează curba de ½ lungimi. ½L = = =

= = = = =

= =

½L = =

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
= 4 (1-0) = 4 ÞL = # 8729 4 2 = 8

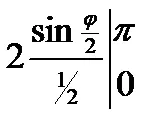
Să presupunem că în formula L = limita inferioară a lungimii arcului rămâne constantă, iar limita superioară este schimbat. Pentru a sublinia acest lucru, limita superioară este notată cu litera x. și variabila de integrare - litera T. Având în vedere faptul că lungimea arcului L este o funcție de limita superioară, obținem:

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare

Conform teoremei asupra derivatului integralei peste marginea de sus a acestei funcții este diferențiabilă și derivatul său este dată de:

De aici arcului diferențialului dl sau, in stenografie, dl = dx. Din moment. apoi dl =

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
. sau dl =

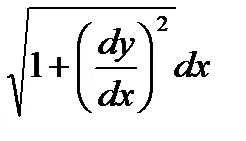
Având în vedere acest rezultat și faptul că diferențiala funcției egală cu tangenta increment ordonată conduce la geometric următor arc sens diferential: diferential dL segment lungimea arcului este tangenta punctul de tangență cu abscisa x la punctul cu abscisa x + dx.

Întrebări pentru auto-control:

Formula 1.Zapishite pentru calcularea lungimii arcului curbei dată într-un sistem de coordonate cartezian.

Formula 2.Zapishite pentru calcularea lungimii arcului definit parametric.

Formula 3.Zapishite pentru calcularea lungimii arcului definit printr-un sistem de coordonate polare.

4. Cum sensul geometric al arcului diferențial?

Sarcini pentru decizia independentă:

Lungimea 1.Nayti a arcului de parabolei pe x = y = 0 = 1 dox.

2. Găsiți lungimea arcului curbei de x =. y = de la t = 0 până la t = 1.

3.Nayti cardioid lungimea arcului r = 2.

Rezolvarea sarcinilor tipice:

Exemplul 1: Găsiți lungimea liniei de la punctul

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare

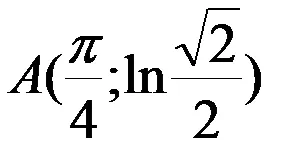
Soluție: Linia specificată în sistemul de coordonate carteziene. Este evident că

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
.

Deoarece intervalul considerat.

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=
Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=
Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=

=

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=
Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=
Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare

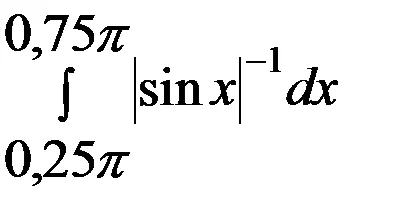
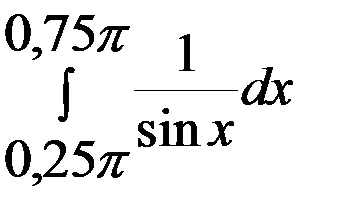
Rețineți că, în calculul integralei am folosit înlocuirea:

Exemplul 2. Găsiți lungimea curbei

.

Soluție: Curba este definită parametric. Este ușor de văzut că

= =

= =

= =

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=
Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
.

Deoarece intervalul, egalitatea

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=.

=

Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare
=
Calcularea curbei lungimii arcului l, definit în sistemul de coordonate polare

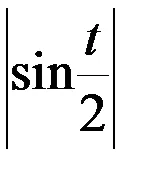
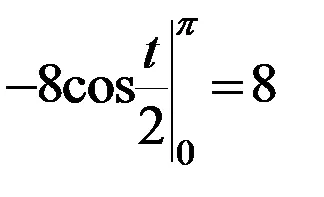
Găsiți lungimea arcului de r = cardioidă a (1 + cos

Soluție: cardioid este simetrică în jurul axei polare. Prin schimbarea unghiului polar de la 0 la. vom obține jumătate din lungimea unui cardioidă:

Întreaga lungime a cardioidă l = 2

Se poate arăta că dată de ecuațiile x = x (t) din lungimea arcului unei curbe spațiale, y = y (t), z = z (t). . Ea are următoarea formulă: