Atomizare cristale covalente de energie

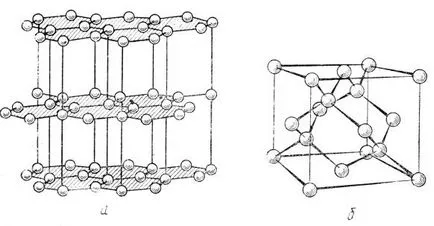
Fig. 37. Structura de grafit (a), structura de diamant (b)

structură ca de grafit (.. vezi figura 37a), este caracteristic nitrura de bor BN, care se află sub mișcări de înaltă presiune în cubi structura de tip diamant de blendă (. Figura 37 b), mediul tetraedric fiecăruia dintre atomii din care indică sp lor 3 - hibridizare. Cele de mai sus că sp confirmă 2 - și sp 3 - orbitali hibride nu sunt proprietatea exclusiva Group atomi IV, acestea sunt posibile la atomii învecinate III și grupele V.

atomi de ambreiaj energetic legate prin forțe covalente măsurate în timpul disocierea unei molecule sau a cristalului de sublimare, pentru a forma un gaz monoatomic. Prin urmare, energia cuplarea covalentă a cristalului poate fi numit atomizare energie. pentru al deosebi de energia latice ionice care este eliberată în timpul formării cristalelor din ionii de gaz.

Problema calculului teoretic al energiei legături covalente este foarte complexă, deoarece se confruntă cu dificultăți în rezolvarea problemelor mecanice cuantice a multor particule. Prin urmare, până în prezent foarte frecvente există diferite metode de evaluare empirică a energiei de legătură covalentă. Experiența arată că energia de echilibru a comunicării homopolare obișnuite este o funcție destul de simplă liniară a lungimii sale. Această relație poate fi exprimată prin ecuația aproximativă: E (kcal) = - 38 R (Â) +136. Pentru elementele din grupa IV (C, Si, Ge, Sn) liber

pe termen lung în această ecuație puțin mai mare: E (kcal) = - 38 R (Â) 143.

Energia de legătură multiplă nu este, de obicei, o simplă bucată de energie de legare obișnuite și multiplicitate. De exemplu, energia necesară pentru a rupe o singură legătură C - C

este de 84, dublu - 141, iar tripla - 187 kcal. Puteți vedea că tt -bond mult mai slab -bond σ, al doilea π-legătura este mai slabă decât prima. Atenuarea π -bond compensată prin scurtarea legăturii multiple în comparație cu simpla -bond σ. Astfel, energia obișnuită, legăturile duble și triple între C și N cuprind 73, 142 și 210 kcal / mol, adică, sunt într-un raport de aproximativ 1: .. 2: 3 datorită scurtarea lungimii legăturilor în acest rând la 0.35 Å .

interacțiuni covalente de energie între diferitele elemente sunt de obicei evaluate pe postulat a mediei aritmetice a lui Pauling:

Se poate remarca faptul că, prin utilizarea unei metode moleculare justificare orbital semi-empirică a egalității aproximativă a fost găsită (12), și datorită simplității sale, este practic foarte convenabil. De exemplu, energia interacțiunii covalente dintre Li și S este egal cu E (S-Li) = 1/2 (28 + 55) = 48 kcal.

5. COMUNICAREA intermediară între ionică și covalentă. Ionicity COMUNICARE.

Electronegativitate și ionicity.

Pentru a acoperi toate tranzițiile posibile între legături ionice și covalente maxime în cele din urmă, Pauling a introdus conceptul în 1932

atom electronegativitate și gradul de ionicity ε legături chimice, care poate varia de la 1 până la 100%, sau legare ionică la 0 - pentru covalenta. atom Electronegativitate caracterizează capacitatea unei molecule (cristal) pentru a atrage electroni. Din această definiție foarte generală, rezultă că o mai mare ER a unui element, cu atât mai mult păstrează perechea de electroni de ansamblu datorită cochilia. Este ușor de înțeles că EA valorile ar trebui să fie mai mare pentru elemente, cum ar fi halogeni (F, CI, etc.) și oxigen, și cel mai puțin - pentru metalul alcalin (Cs, Rb, K, etc.).

Pauling a construit EO la scară printr-un punct de referință arbitrar, astfel,

Elementele EO pentru a doua perioadă de Li la F au fost în valori cuprinse între 1,0 până la 4.0. Valorile EO sunt date în Anexa 1-8.

Intre EE Pauling χ P si χ orbitală EO Mulliken există M

proporționalitate aproximative: χ M / χ n 2,8 eV. De exemplu:

în care parametrul a este de aproximativ 0,2. În cazul în care ε - ionicity, și £ -

gradul de covalency (homopolarity) conexiune. Ecuația (13) reflectă faptul că, odată cu creșterea diferenței EO Δ χ crește conexiunea ionicity.

Ecuația (13) poate fi aplicată în mod substanțial cristale covalente, în care primul număr de coordonare coincide cu valență formale m. E. Pentru fiecare pereche de electroni conexiune localizate. De exemplu, un BN cu o structură stratificată de tip grafit QP = 3 ca valența B și N. Apoi obținem următoarea estimare a ionicity a legăturii în acest cristal:

ε (BN) = l -exp [-0,2 (3,0 - 2,0) 2] = l - exp (-0,2) = 0,18.

Cu alte cuvinte, în legătură cu structura de grafit BN are 18% caracter ionic.

Cu toate acestea, în mai multe cristale ionice CN tipic mai mare de valență formale și perechilor de electroni delocalizați. Pentru astfel de cazuri ecuația (13) dă o limită inferioară de grad de legătură ionicity. Ca Pauling presupus proporțională cu gradul de rezistență delocalizarii (sau multiplicitate) de comunicare s = z / ν. unde z -

valență și ν - numărul de coordonare. Apoi, ecuația (13) ia forma:

ε „(AB) = 1- ξ = 1- (z / ν) exp [- α (Δ χ) 2].

De exemplu, pentru că structura de cristal BN de tip diamant și mediile tetraedrice doi atomi care pot fi obținute din modificarea stratificată la presiuni ridicate, s = 3/4 și ε = 0,38. Pentru moleculele LiF CN = 1 și ε = 0,83 (13) și pentru

cristal QP = 6, s = 1/6 și ε „= 0,97 (14).

Comunicare energie atomizare și energia rețelei de cristal.

Este posibil să se determine calitativ schimbarea (creștere sau scădere) a gradului de ionicity a legăturii în seria de compuși cu un atom comun, de exemplu un număr MX prin înlocuirea numai M (sau doar X) fără dificultate. Apoi, evident, ionicity este mai mică EO mai mare (M) sau mai mare decât potențialul de ionizare al I (M).

Rețineți că, pentru toate cristalele în afară de halogenuri și hidruri, datorită lipsei de afinitate pentru electroni la doi O, S și alți anioni pot fi determinate experimental numai energie E. atomizare care este eliberată în timpul formării atomilor de cristal a gazului în conformitate cu ciclul termochimice :

E = Δ H f + atom Σ Δ H.

Se poate observa că diferența dintre energia zabrele și energia atomizare este egală cu suma algebrică a potențialelor de ionizare și afinitățile de electroni ale tuturor atomilor din cristal.

6. Structura banda de energie a cristalelor:, semiconductori și dielectrice metale.

Structura moleculelor, cum ar fi Li 2. Na2 et al. Este foarte similar cu structura moleculei

H 2. σ-legătură între atomii se realizează datorită suprapunerii s orbitali atomilor. O situație diferită apare în condensarea acestor molecule și formarea cristalelor. Rezultatul este apariția unui imens număr orbitali multicentrice care captează întregul cristal și nivele discrete la care electronii sunt situate în atomi izolați, în formarea difuze de cristal în întreaga bandă de energie așa cum se arată în Fig. 36. Electronii interiori ai atomilor nu interacționează, iar scheletul lor se suprapun puțin, iar zona corespunzătoare este slab scindat. Prin urmare, electronii interni rămân atomii localizate în miezurile lor (curba 4). electroni de valență, din contra,

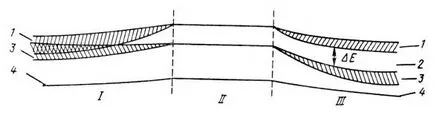
interacționează puternic, iar nivelurile de energie corespunzătoare să ia o bandă largă - banda de valență (curba 3). Deasupra este o zonă care poate fi potențial ocupată de electroni, și este format dintr-o multitudine de nonbonding orbital - banda de conducție (curba 1).

Fig. 38. Dispunerea circuitului zonelor energetice comune: I - metale, III - un semiconductor și un dielectric; 1 - zona de conducere 2 - bandgap, 3 - valență, 4 - stratul interior. II - nivelurile atomului izolat, Δ E - bandgap (2).

În cazul în care între ele există un decalaj de energie nu este ocupat de electroni, este numit decalajul banda. lățimea sa este notat cu E g (sau Δ E); este etichetat cu numărul 2 din Fig. 36.

Banda de valență nu se suprapune cu banda de conducție, atunci când valoarea E g

substanțial mai mare decât energia termică (la temperatura camerei ≈ 0,1 eV). Acest caz corespunde formării dielectricilor și semiconductori. dielectrici exemplare au printre cele două cristale ionice, cum ar fi LIF si CaF2 (Δ E = 12 eV) și includ cristale covalente, cum ar fi diamant (Δ E = 5,3 eV).

semiconductori tipice - cristale cu structuri, cum ar fi diamant-blendă: Ge (0,75), Si (1,12), AlSb (1,60), CdS (2,3 eV). La limita dintre dielectricilor și semiconductori SiC este Karbid Kremniya (3 eV). În cazurile de mai sus, banda de valență a cristalului este complet ocupată. De exemplu, în cazul ionului dielectric (LiF, CaF 2. MgO, NaCl, etc.). Banda Valence este umplut cu electroni localizați pe anionii și o bandă de conducție goală asociată cu orbitalii virane ale cationului. În semiconductori de diamant și cu o structură similară a benzii de valență este complet ocupată de electroni, care pot fi considerate ca fiind localizate pe obligațiuni cu două electroni formate dirijate sp 3 orbitali hibrizi de atomi adiacenți. Acum devine clar de ce toate solidele covalente, se supun regulilor de Hume-Rothery CZK = 8 - N. nu pot fi conductoare. Într-adevăr, în cazul în care această regulă este îndeplinită, fiecare atom are o oportunitate