Amplitudinea oscilațiilor, teoria și calculatoare on-line

mișcări sau vibrații repetate numite procese.

În funcție de natura oscilațiilor poate fi mecanic, electromagnetic, acustic, etc. Alte tipuri de oscilație descrise utilizând aceleași ecuațiile și folosesc aceleași caracteristici, astfel.

Fluctuațiile sunt numite libere (du-te propria lor), în cazul în care acestea apar în detrimentul energiei, care este produsă de sistemul oscilatorie o dată și alte influențe externe asupra sistemului nr.

Cel mai simplu tip de vibrații sunt oscilații armonice.

Ei numesc aceste vibratii vibratii armonice în care o magnitudine oscilant variază în timp conform unui sinus sau cosinus ..

Să oscilații armonice ale unui parametru $ s $, atunci aceste oscilații pot fi descrise prin următoarea ecuație:

în cazul în care $ A = s_ $ - amplitudinea de oscilație; $ $ _0 - ciclic (circular) frecvență de oscilație; $ \ Varphi $ - fluctuațiile de fază inițială (faza la $ t = 0 $); $ (_ 0t + \ varphi) $ - fluctuațiile de fază.

Numita valoare maximă amplitudine a vibrațiilor, care luate în considerare. Deoarece cosinus (sinus like) variază de unu la un minus, atunci valoarea lui $ s $ este în termen de $ -A \ le s \ le $ + A.

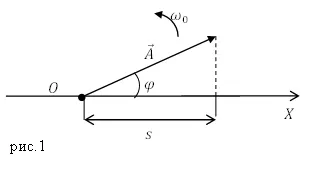
Metoda de rotație vector amplitudine oscilație

oscilații armonice pot fi reprezentate grafic (figura 1), utilizarea metodei diagramelor vectoriale (sau o metodă de rotire a amplitudinii vectorului). În acest scop, din care - axa X punctul arbitrar ales, este numit un punct O, un unghi egal cu faza inițială (unghi de $ \ varphi $), întârziind vectorul $ \ overline $. Lungimea acestui vector este amplitudinea ($ A $) oscilații. Dacă acest vector este rotit cu o viteză unghiulară $ $ _0, proiecția sfârșitul vectorului se deplasează pe axa X și are o valoare de până la $ -A $ $ A $, în care legea valorilor oscilante vor fi cum este ecuația (1). Se pare că oscilații armonice pot fi reprezentate prin proiecție pe o axă a amplitudinilor vectorului $ \ overline $, care este întârziată dintr-un punct arbitrar de pe această axă, la un unghi $ \ varphi $, care se rotește cu o viteză unghiulară în jurul valorii de $ $ _0 punctul selectat.

Exemple de probleme cu soluție

Sarcină. punct material efectuează oscilații armonice, care descrie ecuația: $ x = 0,1_0t + \ varphi) (m) \> $. Este cunoscut faptul că perioada de oscilație a acestui punct este egală cu T = 5 c. Care este viteza de amplitudine ($ v_m $) și amplitudinea accelerației ($ a_m $) din acest punct?

Decizie. În primul rând, vom găsi punctul de frecvență de oscilație ciclică, după cum știm perioada de oscilație:

Cunoscând variația de coordonate definesc modul în care viteza punctului material:

în cazul în care $ x_m = 0,1 $ cu condiția problemei.

Din ecuația (1.2) că amplitudinea vitezei de oscilație a punctului este:

Folosind legea ratei de schimbare, vom obține legea de schimbare a punctelor de accelerație:

Din legea (1.3) că amplitudinea punctului de accelerație este egală cu:

Sarcină. Prin primăvară orizontală, coeficientul de elasticitate egal cu $ k, $ atașat de masă $ M $ pasă, acesta. Mingea este pe o masa buna, peste care se pot deplasa fără frecare. Bullet zboară orizontal și lovește mingea devine blocat în ea. viteză botul înainte de impact este de $ v_0 $, glonț greutate $ m $, viteza sa de impact îndreptat paralel cu axa arcului. Care este amplitudinea oscilațiilor mingea cu un glonț? Masa de primăvară și de aer trageți neglijat.

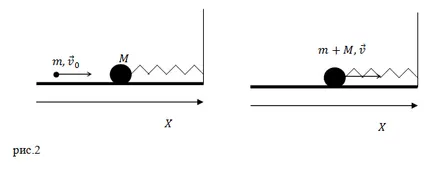
Decizie. Scriem legea conservării impulsului pentru un sistem de minge - bilă (pentru a lovi) și o minge cu un glonț imediat după impact:

Din figura 2, rezultă că (2.1) pot fi transformate în:

De la (2.2) ne exprima viteza mingii imediat după un impact glonț:

Sistem de glonț minge, starea dezechilibrată dintre gloanțe a lovit. Se face oscilații armonice disponibile. Energia cinetică este transformată în energie potențială de arcuri comprimate. Pentru cele două stări ale sistemului (primul stat - viteza maximă de mișcare a sistemului; a doua stare de comprimare maximă a arcului), în conformitate cu legea de conservare a energiei, vom scrie:

în cazul în care $ x_m $ - amplitudinea oscilației mingea cu un glonț. Substituind valoarea vitezei (2.3) în (2.4) și amplitudine expresă: