WolframAlpha în metoda de matrice rusă pentru sisteme de ecuații algebrice liniare rezolvarea
Metoda prin matrice pentru sisteme de ecuații algebrice liniare rezolvarea
Solicitare a rezolva. care a fost utilizat anterior. pentru a obține o soluție a unui sistem de ecuații algebrice liniare (SLAR) din Wolfram | Alpha, de fapt, este o cerere universal pentru rezolvarea ecuațiilor și sistemelor lor din Wolfram | Alpha. De fapt, pentru rezolvarea unui sistem de ecuații algebrice liniare se aplică numai în cazul în care sistemul este stabilit într-un mod natural: după cererea de a rezolva toate ecuațiile sistemului sunt listate, separate prin virgula. Această metodă este bună, pentru că ne permite să rezolve nu numai sigur, dar, de asemenea, sistemul incert - în termeni generali.
Pentru a rezolva anumite sisteme de ecuații algebrice liniare este, de asemenea, metoda de matrice utilizat.
Wolfram | Alpha pentru sisteme de ecuații algebrice liniare ale metodei matricei de rezolvare este o cerere specială LinearSolve. urmată de matricea coeficienților vectorului (matricea coloanei) membri liberi.
Pentru a înțelege sintaxa de interogare caracteristici LinearSolve. studia exemplele următoare.
Pentru a începe, considerăm soluția de sisteme omogene de ecuatii algebrice liniare. La solicitarea LinearSolve intră coeficienții matricei sistemului și vectorul zero al termenilor liberi. obținem:
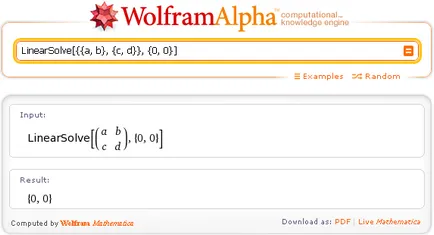
Aici Wolfram | Alpha oferă o soluție banală.
De asemenea ușor Wolfram | Alpha are soluția trivială a sistemelor omogene de ecuatii algebrice liniare de dimensiuni mai mari.

Acum, uita-te la soluția sistemelor neomogene de ecuații algebrice liniare.
După LinearSolve cerere introduce matricea coeficienților și un vector nenul membri liberi. Ca răspuns pentru a obține un vector de necunoscute. Iată două exemple.

