Unghiul dintre linia dreaptă și planul
# 10070; Unghiul dintre vectorul și linia
# 10070; Unghiul dintre linia dreaptă și planul
# 10070; Unghiul dintre planurile
3. Probleme cu analiza
4. Sarcini pentru decizia independentă
Pentru a rezolva problema de a găsi unghiuri, introducem conceptele de bază.
Dacă printr-un punct în spațiu a avut loc trei linii perpendiculare reciproc, fiecare dintre ele este selectat, iar direcția de selectare a unității de segmente, se spune că un sistem de coordonate cartezian în spațiu.
Drepte, cu zone selectate acestea sunt numite axe de coordonate. dar punctul lor comun - originea. De obicei, este notat cu litera O. Axele sunt desemnate după cum urmează: Ox, Oy, Oz - și au un nume: axa x, axa y, axa Z, respectiv.
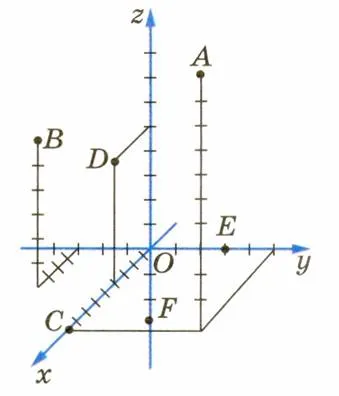
Figura prezintă șase puncte cu coordonate:
A (9, 5, 10) C (9; 0; 0) E (0, 3, 0)
In (4, -3, 6) D (4, 0, 5) F (0, 0, -3)
Acum, ia în considerare vectorii. Orice vector poate fi descompus în coordonate vector, t. E. Prezent în formă. în cazul în care. vectorii unitare și coeficienții de dilatare x, y, z sunt unic determinate.
Coeficienții x, vectori y și z în descompunerea vectorului coordonatelor vectorilor nazyvayutsyakoordinatami în acest sistem de coordonate.
Dată fiind vectorul. Lungimea vectorului (| |) este rădăcina suma pătratelor coordonate:
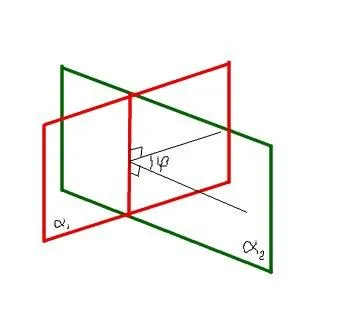
Două avioane intersectate formează două perechi egale între ele unghiuri diedre. Unghi valoare diedru măsurat unghiul liniar corespunzător.
Pentru a construi un unghi diedru liniar. trebuie să luați pe un plan care traversează linia un punct arbitrar, și în fiecare plan să-și petreacă acest punct fasciculul perpendicular pe linia de intersecție a avionului. Unghiul format de aceste grinzi și un unghi diedru liniar:
Mărimea unghiului dintre planuri este o cantitate mai mică unghiul diedru.
Găsirea unghiurilor prin produsul scalar
Unghiul dintre vectorii
Produsul vectorilor și pot fi găsite prin pliere produsele corespunzătoare coordonatele acestor vectori:
Prin definiția produsului scalar al vectorilor exprimat prin formula
. unde este unghiul dintre vectorii.
Prin urmare, unghiul dintre vectori este egal cu:
Găsiți unghiul dintre vectorii și
Soluție: Găsim produsul interior al vectorilor:
= 3 x 4 + 4 + 4 · 0 · = 12 + 2 16 + 0 = 28.
Să ne găsim module vectori:
Am găsit unghiul dintre vectorii:
Unghiul dintre drepte
Pentru a calcula unghiul dintre cele două linii drepte este folosit ca produsul interior. Vom introduce noțiunea de vectorul de direcție al liniei. vector nenul este numit un vector de direcție a unei linii drepte l, dacă aceasta este fie l direct, sau pe o linie paralelă cu l.
Lăsați vectorii direcție de linii a și b. Notăm prin unghiul dorit dintre aceste linii. Pentru a rezolva problema suficient pentru a găsi. deoarece valoarea permite de a găsi unghiul # 945;.
Introducem notația: # 1138; unghiul dintre acești vectori, atunci (dacă) sau # 945 = 180 ° - (dacă # 1138;> 90 °).
Deci, fie. fie. În orice caz. precum și # 945; ≤90 °, atunci. și. Prin urmare. Folosind formula de a găsi unghiul dintre vectorii, obținem:
Se calculează unghiul dintre liniile
Ghidajele directe vectorii au coordonate:
Conform formulei de unghiul dintre liniile drepte găsi
Unghiul dintre linia dreaptă și planul
Ecuația plan este după cum urmează:
În această ecuație, coeficienții plane a, b și c - coordonatele vectorului normale la planul (adică, vectorul perpendicular pe planul).
Vector direcțională linie vector l. sinusul unghiului # 946; între linia l și planul # 945; este egal cu cosinusul unghiului # 947; între normal
() La planul ghidului și vectorul direct (. Ca
# 946; + # 947; = 90 °, sau care este,
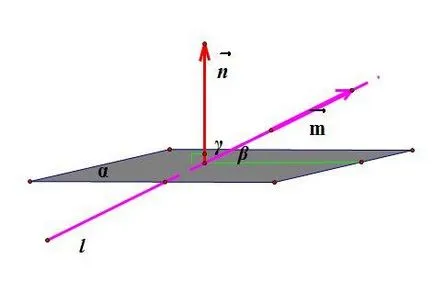
Aceasta este sinusul unghiului # 946; între o linie dreaptă, a cărei vector de direcție și planul are coordonate definit de ecuația
calculat după cum urmează:
Unghiul dintre planurile
Pentru a echivala avionul. cunoscând coordonatele unui plan și un vector normal de avion. Puteți utiliza următoarea formulă:
Să planul nostru și dat de:
cosinusul unghiului # 945; între planele situate pe următoarea formulă:
Ca răspuns, suntem înregistrați. deoarece magnitudinea unghiului dintre planuri este unghiul de cantitatea menshegodvugrannogo. Asta este, cosinusul unghiului dintre planele este cosinusul unghiului dintre normalele avioane.
Găsiți unghiul dintre ploskostyamii
Decizie. Substituind în formula de calcul a unghiului dintre planele coeficienților respectivi: