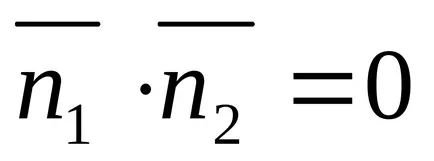Unghiul dintre drepte
Condiția de paralelism a două linii. Notăm două linii
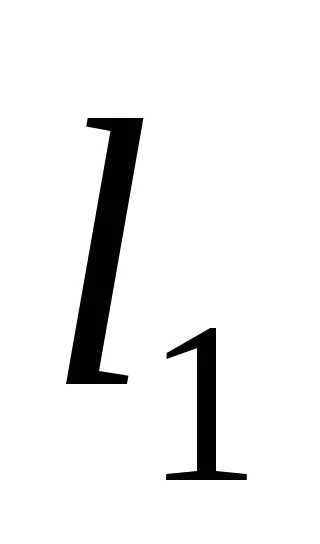
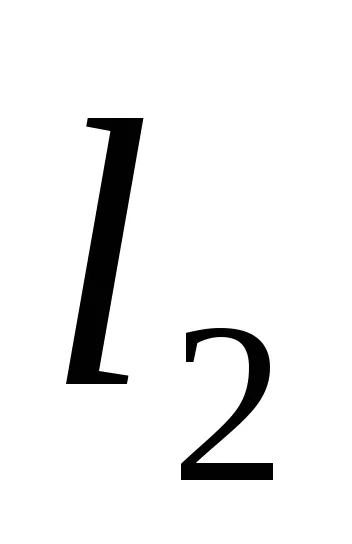
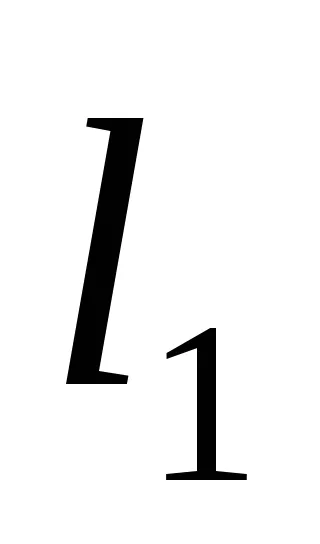
Starea de perpendicularitate a două linii drepte:
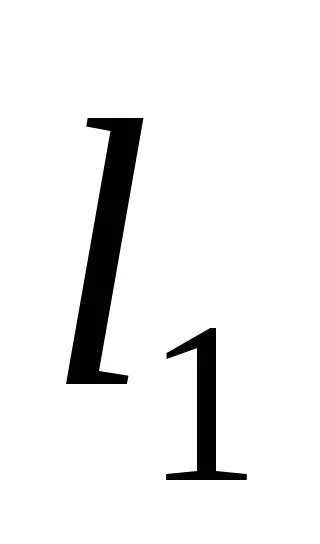
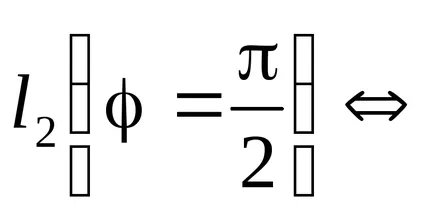
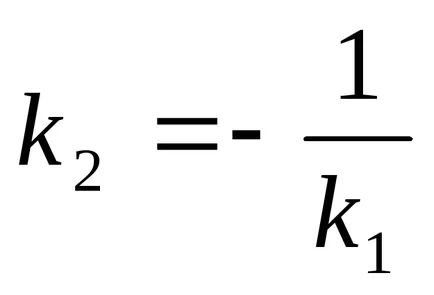
Ecuația generală a liniei
Teorema. Într-un sistem de coordonate cartezian, fiecare linie este definită prin ecuația primului grad și invers, fiecare ecuație de gradul întâi definește o linie dreaptă.
Dovada. Să presupunem că există o directă
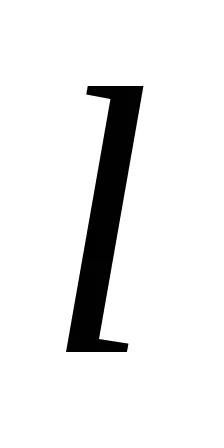
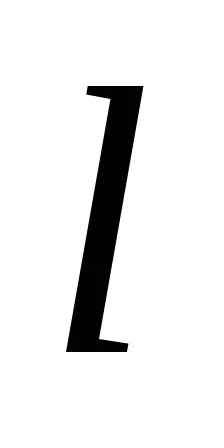
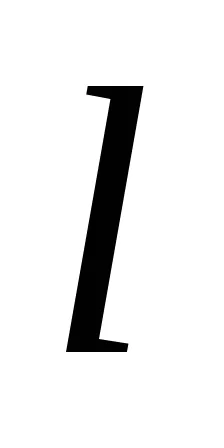
Înapoi. Luați în considerare ecuația
a). Dacă B ≠ 0, putem scrie
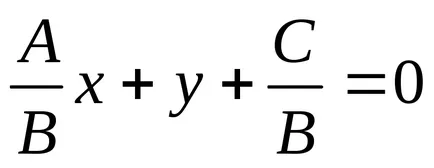
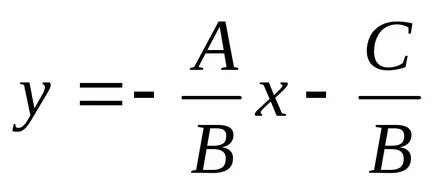
denota
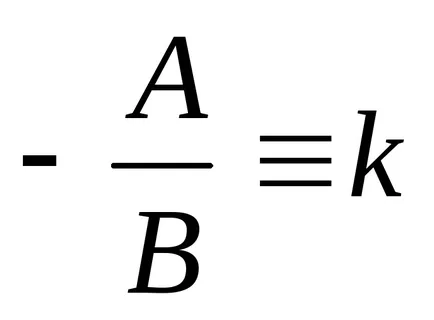
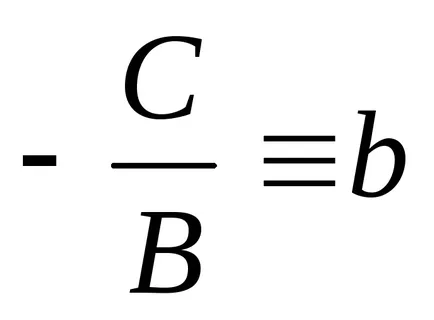
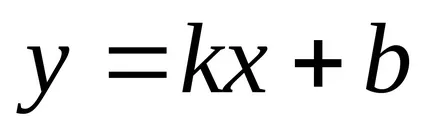
b). Dacă B = 0, atunci A ≠ 0.
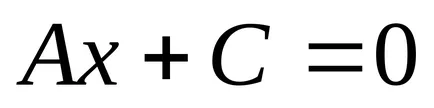
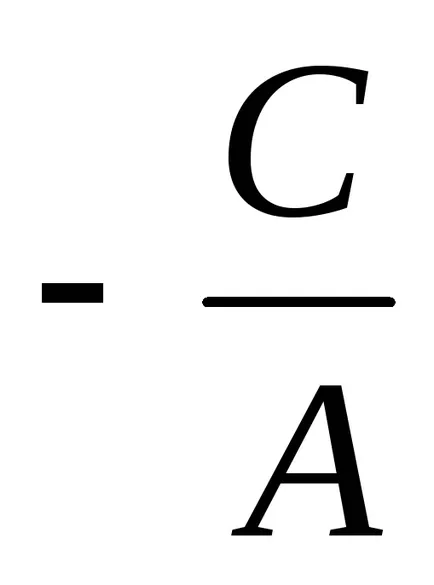
lăsa
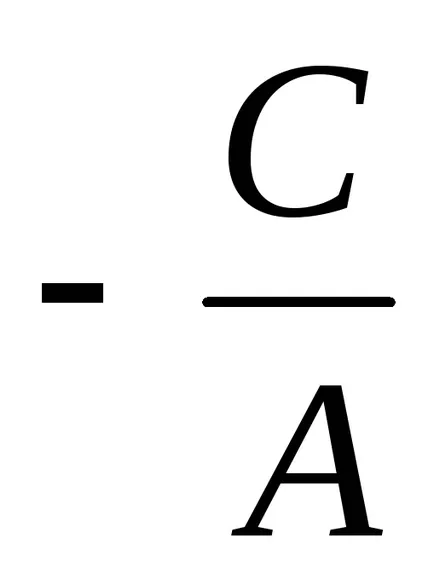
Ecuația Ax + By + C = 0 se numește ecuația generală linie. deoarece determină toate tipurile de linii, fără excepție.
Ecuația incompletă a primului grad
Luați în considerare trei cazuri, atunci când ecuația este incompletă.
C = 0 => Ax + By = 0 - linia trece prin origine.
B = 0 (A ≠ 0) => C = Ax + 0 - linie paralelă cu axa y.
A = 0 (V ≠ 0) => By + C = 0 - linie este paralelă cu Ox.
Ecuația liniei „în bucăți“
Să considerăm ecuația Ax + By + C = 0, gdeA ≠ 0, ≠ 0 și C ≠ 0.
Converti la forma Ax + By = C și se împarte la (C):
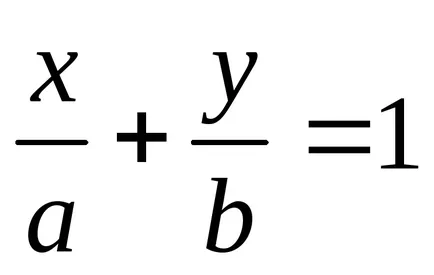
Numerele a și b în ecuația (8) au un sens geometric. Aceasta este intercepta linia dreaptă pe axele de coordonate.
Sigur. Găsim coordonatele punctelor de intersecție cu axa x:
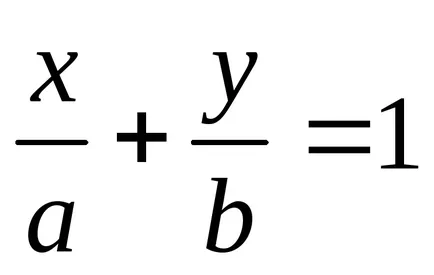
In mod similar, lungimea segmentului este tăiat cu o linie dreaptă pe axa y.
Un studiu comun al ecuațiilor două linii
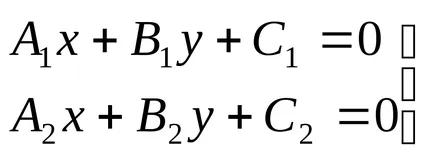
Fiecare ecuație definește linia în plan. Soluția comună a acestor ecuații definește un punct comun al acestor linii.
1). lăsa
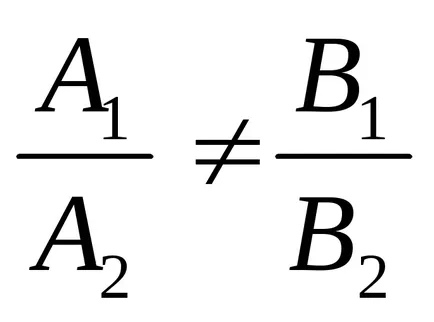
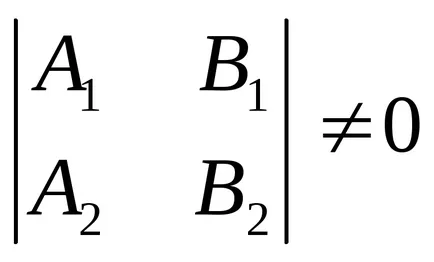
Acest lucru înseamnă că liniile se intersectează la un moment dat. Coordonatele punctelor de intersecție sunt date de Cramer.
2). lăsa
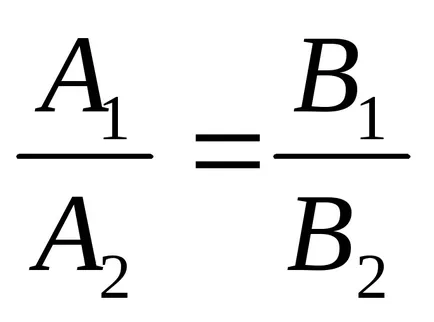
a)
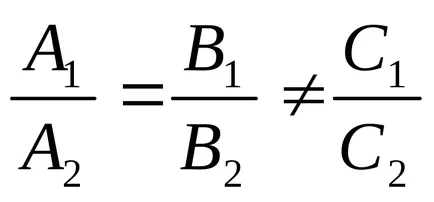
b)
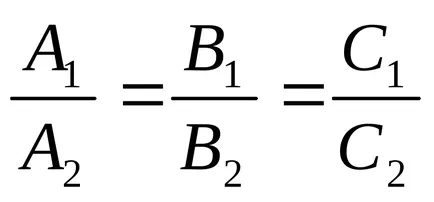
Două ecuații definesc o linie dreaptă, în cazul în care coeficienții sunt proporționale.
Normal la linia dreaptă
Lăsați linie dreaptă L este dată de ecuația generală:
Să m. M0 (x0, y0)
Expresia (11) poate fi privit ca un produs scalar a doi vectori:
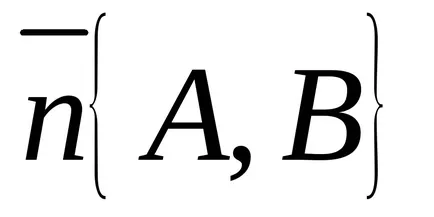
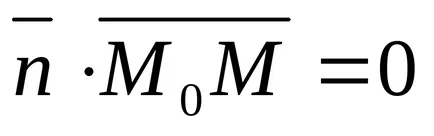
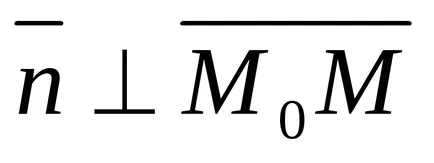
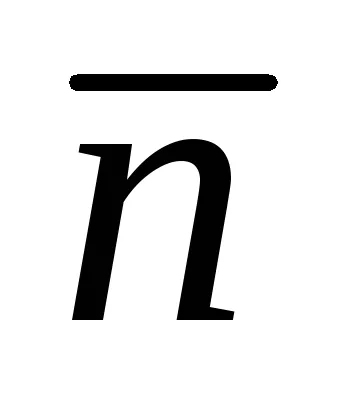
Unghiul dintre două linii
Normal la dreapta:
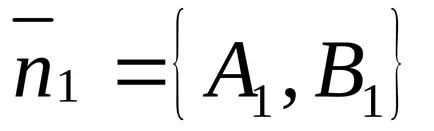
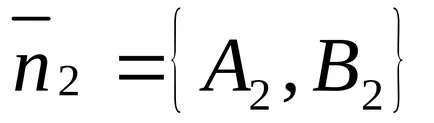
Unghiul dintre liniile poate fi definit ca unghiul dintre normalele la aceste linii:

Apoi, starea de linii paralele - o stare normală de coliniarității:
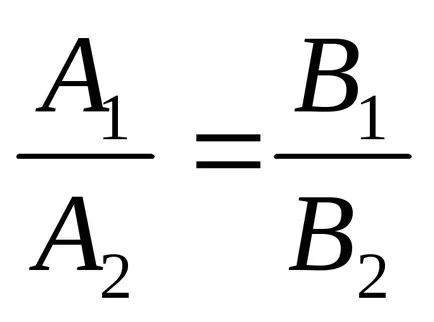
Starea de linii perpendiculare - este normalele perpendiculare: