Traiectoria, lungimea căii, vectorul deplasare
Trecerea în timp de la un punct la altul, corpul (punct material) descrie anumite linii, care se numește traiectoria mișcării corpului.
Sunt cinci tipuri de mișcare a corpului rigid, și, respectiv, cinci tipuri de traiectorii:
- mișcarea translațională a corpului în cinematica mișcare rectilinie a unui punct corespunzătoare;
- Aceasta corespunde cu mișcarea de rotație a mișcării corpului unui punct de pe circumferință;
- mișcarea corpului plat corespunde mișcării unui punct pe un plan;
- mișcarea corpului sferic corespunde mișcării unui punct de pe suprafața sferei;
- libera circulație a corpului corespunde cu mișcarea unui punct pe o traiectorie arbitrară.
Determinarea poziției punctului de coordonate x = x (t), y = y (t) și z = z (t) și vectorul raza $ \ overrightarrow \ stânga (t \ dreapta) $. $ \ Overrightarrow $ - poziția vector raza punctului de la momentul inițial
Legea mișcării definind o poziție a unui punct material în spațiu, în orice moment dat poate fi determinată fie coordonate mod, prin dependența de timp a coordonatelor x = x (t), y = y (t), z = z (t), sau metoda vector, prin dependența de timp a razei vectorului $ \ overrightarrow = \ overrightarrow \ stânga (t \ dreapta) $, de la origine la punctul dat (fig. 1.1).
Mutarea $ corpului \ overrightarrow = \ triunghi \ overrightarrow> = \ overrightarrow- \ overrightarrow $ numit direcția segmentului de linie care leagă punctele de început și de sfârșit ale traetktorii corpului. L este distanța parcursă lungimea traseului parcurs de organismul peste ceva timp t.
Distanța parcursă $ l $ și vectorul de deplasare $ \ $ overrightarrow la mișcarea corpului krivolineynom. $ A $ și $ b $ - puncte inițiale și finale ale căii
După cum se vede din figura 2, mișcarea a corpului într-un vector curbat deplasare unitate cale este întotdeauna mai mică distanța parcursă.
Mutarea - cantitatea vector. Acesta direcționat segment.
Cale - o cantitate scalară. Acest număr.
Suma a două mișcări succesive de la punctul 1 la punctul 2 și de la punctul 2 la punctul 3 se deplasează de la punctul 1 la punctul 3 (figura 3):
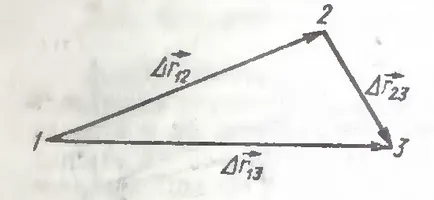
Figura 3. Suma a două mișcări succesive.
Dacă în momentul în vectorul raza punctului de material t este $ \ overrightarrow $ (t), iar la momentul t $ + \ triunghi t $ are $ \ overrightarrow $ (t $ + \ triunghi $ t). apoi se deplasează $ \ triunghi \ overrightarrow $ în timpul intervalului de timp $ \ triunghi t $ Suma: $ \ triunghi \ overrightarrow = \ overrightarrow $ (t $ + \ triunghi t) - \ overrightarrow $ (t)
Mutarea $ \ triunghi \ overrightarrow $ există o funcție de timp t: $ \ triunghi \ overrightarrow = triunghi \ overrightarrow \ (t) $