Subiect 9 convecție naturală
convecția naturală sau liberă apare la gaze sau lichide cu o densitate variabilă în domeniul forțelor de masă, de exemplu, în câmpul gravitațional al Pământului. Acest lucru dă naștere la forța de flotabilitate (Arhimede). În condiții reale, mecanismele de transfer de căldură naturale și induse poate funcționa simultan. Raportul dintre fluxul de căldură cauzată de convecție naturală și forțată, forțele de flotabilitate măsurat raportul proporțional Δρqh (gdeΔρ - diferența de densitate la puncte separate rasstoyaniemh, q - accelerație gravitațională) și forța proportsionalnyhρU2 inerție. Acest raport se numește numărul Richardson.

La schimbări relative cu o densitate scăzută

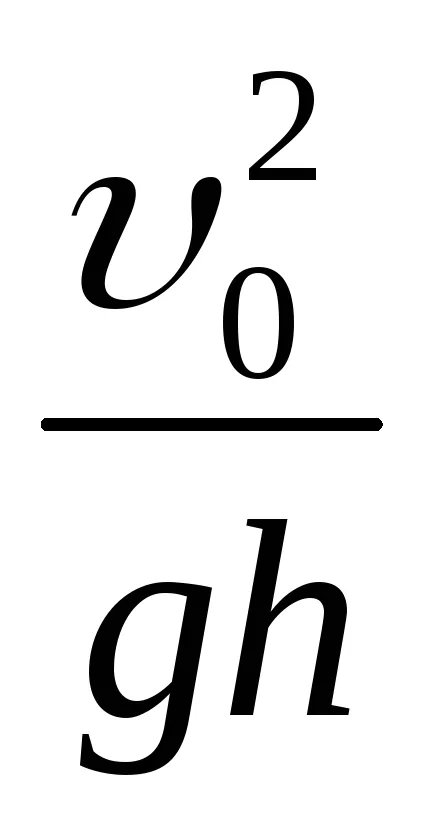
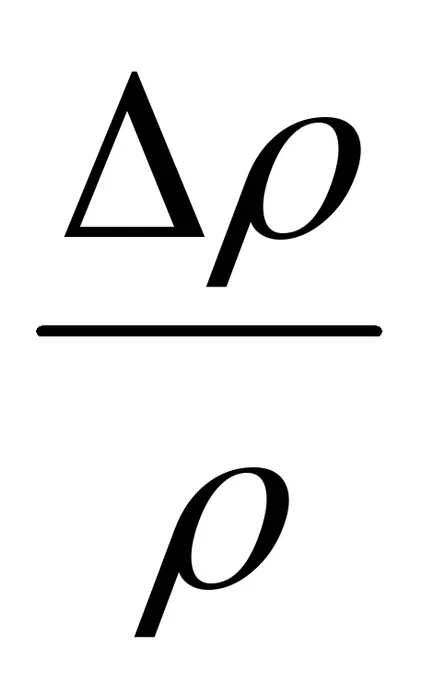

Diferența de densitate Δρ = ρ - ρ0 este exprimată ca diferența de temperatură
,
unde

Criteriul de determinare a intensității schimbului de căldură prin convecție naturală, este numărul Grashof, care caracterizează forțele ratio flotabilitatea și viscozității
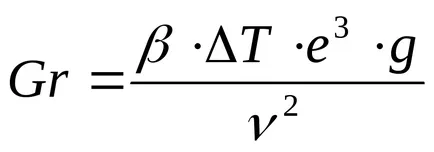
În prelucrarea datelor experimentale privind transferul de căldură prin convecție naturală este, de asemenea, utilizat de numărul Rayleigh
Boussinesq schimbare a modelului în densitatea este luată în considerare numai în determinarea forțelor de masă de flotabilitate.
unde
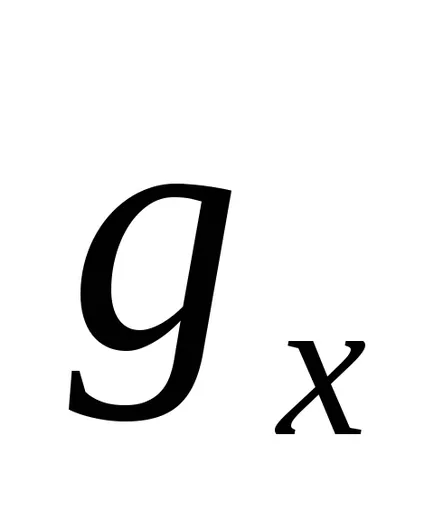
Apoi se furnizează ecuația de mișcare în proiecția plană pe axa x
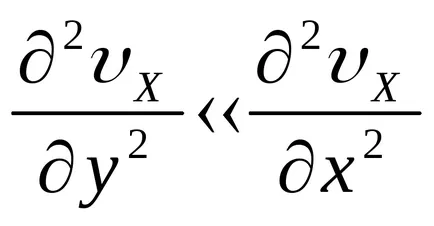
Este scris sub forma
convecția naturală lângă pereții solizi ai unui volum mare are proprietățile stratului limită. Cu toate acestea, câmpul de viteză este direct legată de distribuția densității de temperatură. Luați în considerare flux laminar în stratul limită în apropierea plăcii verticale încălzite într-un spațiu infinit.
Ecuațiile pentru stratul limită de curgere liberă prin convecție staționară are forma:
- Ecuația mișcării în proiecția pe axa x
Pentru a rezolva (9.3) - (9.5) în urma Pohlhausen, se duce la noile variabile
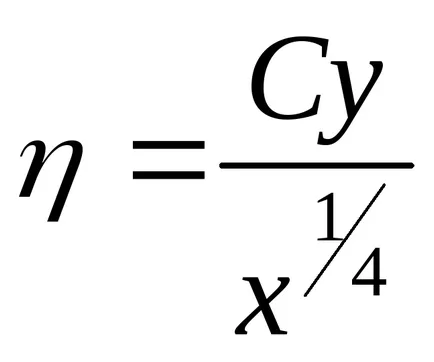

unde ψ (x, y) - funcția curentă,
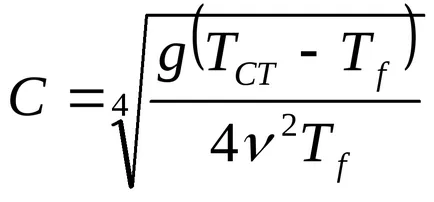
Proiecția vitezei în aceste variabile sunt exprimate după cum urmează:

Apoi, din (9.6), (9.7), obținem două ecuații diferențiale:

Sistemul (9.8) este rezolvată cu următoarele condiții limită
Ecuațiile (9.8) cu condiții la limită (9,9) sunt rezolvate numeric sau prin raporturi integrale. Soluție numerică obținută după trecerea la variabilele fizice inițiale

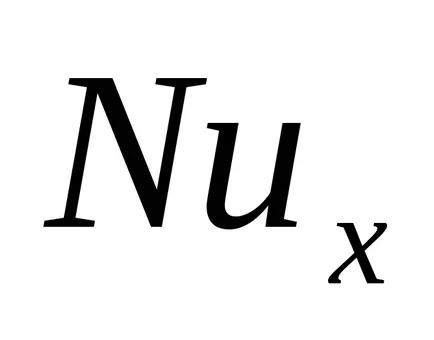
iar numărul mediu
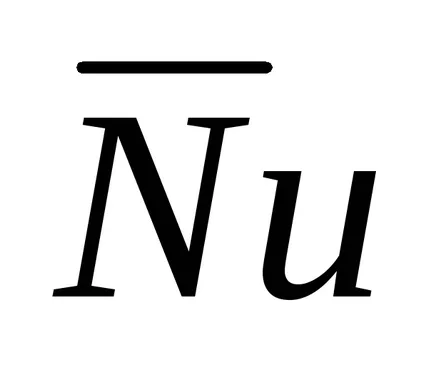
Pentru calcularea plăcii de transfer termic montat cu înclinarea între suprafața inferioară a plăcii de transfer termic și cp vertical
Pentru placa încălzită îndreptată în sus
Pentru convecție naturală turbulentă este setată dependența criterială
La calcularea transferului de căldură convectiv prin mecanism convecția naturală la plăcile verticale, cilindrii orizontale și verticale, bile formula aplicabilă
în care dimensiunea caracteristică pentru plăcile verticale și cilindrilor - înălțimea și a cilindrilor orizontale și bile - diametrul, parametrii fizici sunt determinate de
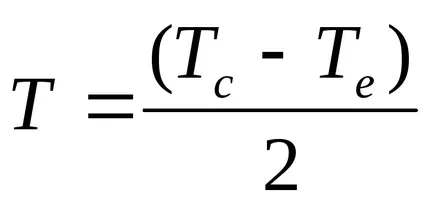
Empirică constantele C și n diferite în diferite domenii ale numărului Rayleigh:
- psevdoteploprovodnosti (10-3 modul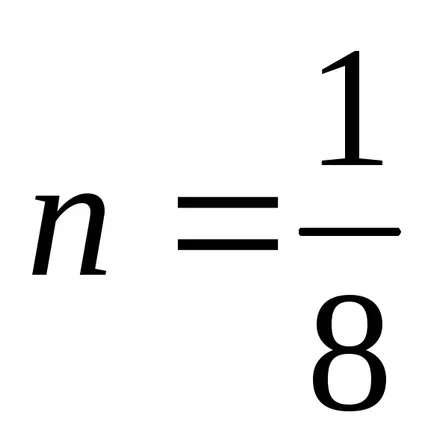
- regim laminar format
- condiții tranzitorii și turbulente
Când convecție naturală într-o grosime a stratului spațiu închis comensurabil cu dimensiunile spațiului. Prin urmare, transferul de căldură depinde în mod esențial de forma acestui spațiu.
Într-un pat fluid sau gaz cu o temperatură T2 mai mic> T1. situată între două plăci orizontale plane, separate printr-un rasstoyaniiδ. convecție naturală are loc atunci când

în care - numărul Rayleigh Rakr = 1700. (9.17)
Atunci când există un flux târâtor cu viteze mici. Hexagon format în termenii celulei. In experimente cu diferite lichide majoritatea creștere lichid în centrele celulelor și coborâre pe fețele. In experimentele cu gazele este exact invers, care este asociat cu o creștere a viscozității cu creșterea temperaturii. vâscozitatea fluidului scade odată cu creșterea temperaturii. Ecuația de transfer termic adimensional are forma
unde


Modul avansat laminar de convecție se observă la
, , O structură alternării arbori lungi orizontale. Numărul Nusselt este definit de relația
În modul de tranziție,
In formulele (9.17) - (9.20) ca temperatura adoptată definind
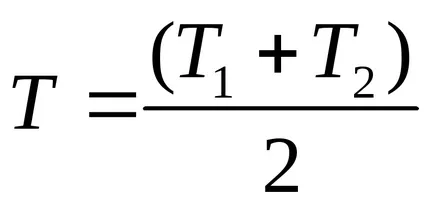
Fluxul de căldură specific prin fantă considerată ö gap este dată de
Trebuie remarcat faptul că soluția numerică a ecuațiilor Navier-Stokes sunt în acord satisfăcător cu datele experimentale generalizate (9.17) - (9.20).
Luați în considerare convecția aerului în fanta de fantă verticală δ între plăci plane vysotoyh (h / δ = 10), având temperatura T1 și T2> transfer de căldură T1 priintensivnost este determinată de conductivitate termică. Modul Prinablyudaetsya atunci când începe să formeze un flux laminar. În diapazonepoyavlyaetsya strat laminar limita modul dezvoltat. Tranziția de la laminar la strat turbulent caracterizat prin starea. la

Pentru lichide cu picăturii

Pentru aer la și
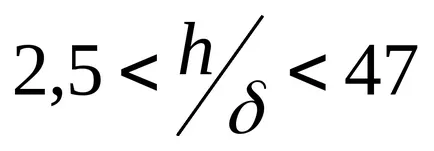
In formulele (9.22) și (9.23) dimensiunea caracteristică - lărgimea ö gap,
