Soluție grafică a problemei de programare liniară

După cum se știe, problema generală de programare liniară constă în găsirea valorile variabilelor care satisfac anumite constrângeri liniare și pentru a asigura cea mai mare valoare (cea mai mică) a funcției liniare specificată. De exemplu, cerința:

În rolul cantităților necunoscute pot fi, de exemplu, volumul producției (de pantofi, dispozitive viziune de noapte și microscoape), distribuirea de numerar la lichidarea de locuințe dărăpănate și construirea de facilități de sănătate, cu un tiraj de poezii M. Yu Lermontova și „conspirație împotriva deochiului.“; restricții legate de consumul de materiale, disponibilitatea beneficiilor pentru anumite tipuri de publicații, condițiile de piață sau preferințele personale, și funcția obiectiv L (X) poate determina profitul din bunuri fabricate sau valoarea fondurilor netrase.

Puteți descoperi că problema este de nerezolvat - nu există nici un plan (restricții se contrazic reciproc). Poate singurul plan sau o mulțime (multe) planuri, printre care este necesar pentru a găsi cele mai bune (optime), care dă profitul maxim (satisfacție morală, grad de apă de purificare) sau un cost minim (reclamații publice, în timp ce deșeurile de lemn, etc.).

Dimensiunea sarcinilor reale de obicei ridicate (de la zeci la câteva sute). Aici vom prin exemplul problemelor bidimensionale pentru a da cititorului o reprezentare clară, grafică de a fi rezolvată prin programe liniare (presupunând că fiecare persoană este în măsură să se bazeze pe o bucată plană de hârtie și să ia construcția de spațiu tridimensional din jurul nostru). Prezența unor astfel de reprezentare poate ajuta, de asemenea, în generalizarea constatărilor bulshey probleme la scară.

În mod firesc, pentru rezolvarea problemei, este de dorit pentru a obține mai întâi o idee despre varietatea de planuri (soluții acceptabile), și numai apoi din setul de a alege cele mai bune (în ceea ce privește obiectivul).

Deoarece sistemul limitează programarea liniară bidimensională determină setul puncte ale planului sau culcată linii drepte, sau avioane și jumătate delimitate de aceste linii, setul de planuri poate fi reprezentat printr-un punct, o parte dintr-o linie dreaptă, o siluetă care seamănă cu un poligon convex, dar nu o elipsă, semiluna sau alt obiect curbat.

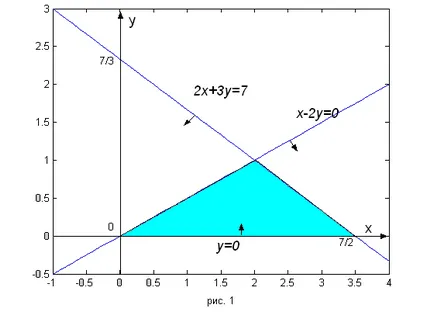
Deci, în cazul în care problema se limitează la a descrie termenii 2x + 3Y ≤7. y ≥0. x- 2y ≥0. construct original, linii drepte corespunzătoare (2x drepte + 3y> = 7 cu axele de coordonate ale punctelor de intersecție, linie dreaptă y = 0 coincide cu 0x axelor; directiona x- 2y = 0 trece prin originea și este, de exemplu, un punct cu coordonatele x = 2. y = 1). Procedând astfel „complex“ de construcție, pentru a afla ce fel de o jumătate de plan este acceptabil pentru inegalitatea corespunzătoare, care este suficient pentru a lua oriunde în avionul care nu se află pe o linie dreaptă, și să verifice constrângerile. De exemplu, pentru a verifica dacă o primă limită (corespunzătoare liniei nu trece prin origine) poate lua punctul (x = 0. y = 0) pentru a se asigura că 2 · 0 · 0 + 3 <7. Следовательно, эта точка со всеми ее «соседями» до прямой линии (полуплоскость, её содержащая) соответствует неравенству 2x+ 3y ≤7. На рис. 1 приемлемые полуплоскости выделены стрелками и общая их часть (множество точек, удовлетворяющих всем трем условиям; множество планов) представлена выделенным здесь треугольником.

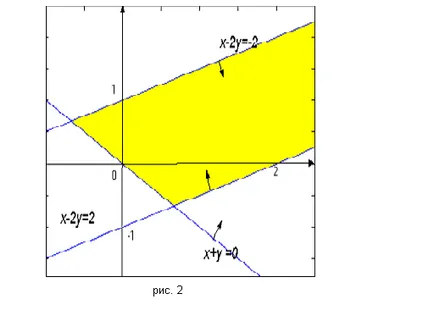
Construirea semiplanul corespunzător adecvat trei drepte și de a afla, am descoperit că o mulțime de planuri - poligon nelimitat (triunghi, dintre care un nod „trimis la infinit“) prezentate în Fig. 2.

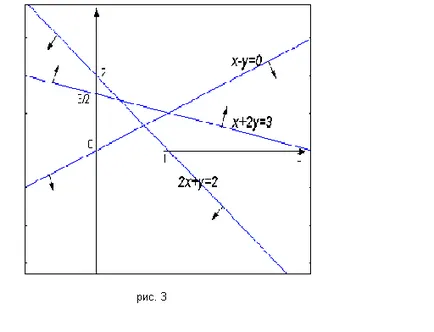
Dacă luați sistemul de constrângeri de forma x + 2y ≥3. 2x + y ≤ 2. X-Y ≥ 0. este ușor de văzut (figura 3.) Că nici un singur punct, care să satisfacă toate cele trei condiții, nu se poate găsi - constrângeri contradictorii (set-up de gol).

Ce concluzii pot fi trase din aceste exemple?

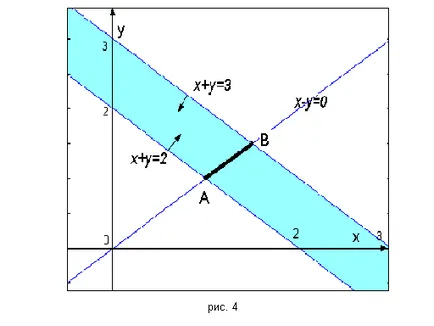
O multitudine de planuri bidimensionale ale problemei de programare liniară este un poligon convex (limitat sau nelimitat), un segment de linie dreaptă (limitat sau nelimitat) litera sau absentă din cauza constrângerilor contradictorii (fără forme curbate sau non-convexe).

Acum, amintindu scopul nostru, să ne întrebăm: ce fel de găsit un set de planuri este optimă (oferă cea mai mare valoare (cel puțin) din funcția noastră obiectiv)?

Egal schematic nu numai o pluralitate de planuri în plan (x, y), dar funcția țintă z = L (x, y), spațiul tridimensional plan imagisticii unde z valoare reprezintă îndepărtarea acestui plan din planul (x, y). Evident, cel mai mare și cel mai puțin distanța de la multitudinea de planuri este cazul în unele dintre nodurile sale, dar nu și în punctele sale interne (Fig. 5).

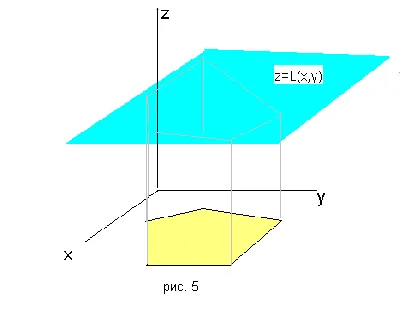
Dacă această imagine nu vă asigur în acest (sau uitați că ecuația planului în spațiul tridimensional poate fi reprezentată printr-o ecuație liniară de α · x + β · y + γ · z = c), atrage conceptul de ajutor al funcției de gradient - un vector, compus din derivații săi parțiale, care indică direcția cea mai mare creștere a funcției, în vecinătatea punctului. Pentru funcții neliniare ale gradientului variază de la un punct la altul. De exemplu, dacă f (x, y) = x2 + xy. gradf (x) = 2x + y, x> la diferite puncte își schimbă orientarea. În cazul unei funcții liniare, constituind gradientul acestuia coincide cu coeficienți săi, de exemplu gradL (x, y) = 2x + 5y> = 2, 5> și gradientul rămân neschimbate la toate punctele (în special, la toate punctele de un set de planuri).

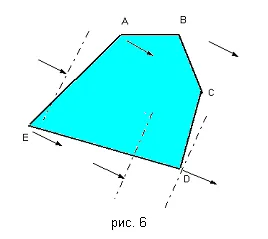
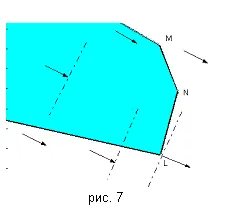
Fig. 6 am arătat o mulțime de planuri de sarcini (ABCDE poligon) și arată direcția săgeții gradientului. Alegerea orice punct intern al setului de planuri, vom vedea că, în imediata apropiere a acestuia se poate găsi un alt punct (diferența în gradientul sau invers) c bulshim (mai mică) valoarea L (x, y). Evident, în acest caz, se atinge maximul de la punctul D. și punctul -sa minim E. Desigur, în cazul în care gradientul este perpendicular pe o față a setului (segmentul de linie), extremum este atins la toate punctele segmentului (în special, la capetele sale).

Acest lucru sugerează că, atunci când căutarea punctelor extremum (maxim sau minim) ale funcției liniare (planurile optime) este suficient să se ia în considerare numai setul de sus a planurilor. dar nu și punctele sale interne. Mai mult decât atât, în cazul bidimensional pentru suficient de precise pentru a scala construcțiilor nu se poate trece prin toate nodurile (numărul desigur, dar poate fi relativ mare), și imediat vizibil la extrem.

Notă în Fig. 7. în cazul în care o mulțime de planuri este nelimitat. Prin construirea gradientul funcției obiectiv, este ușor de văzut că maximul este atins la apex L. întrucât funcția minimă nu este limitată (cel puțin L (x, y) → -∞). Acest exemplu arată că, în cazul unui set de planuri nemărginită poate arăta neogranichennostL (x, y) la maxim, minim, sau ambele criterii.

Astfel, soluția grafică a bidimensionale programe liniare pot duce la următoarele rezultate:

• planul optim găsit (probabil mai multe);
• a relevat absența planului optim (sarcini constrângeri contradictorii sau funcția țintă nu este limitată din cauza set nemărginită de planuri).

Dacă mai aveți dubii, consultați exemplele de mai jos (aici am primit în schimb în simbolurile matematice școală x și y folosind simboluri x1 și x2, sperăm că această schimbare nu vă va duce în confuzie).

Exemplul 1. Am rezolva problema de maximizare

Decizie. Găsiți setul de soluții (planuri) problemă fezabilă, și anume, setul de puncte (x1, x2), care satisface limitările sistemului specificate (1) - (5), care construiesc jumătate plan corespunzător constrângerile problemei și determină suprafața totală a lor.

Noi luăm prima dintre condițiile și construi o linie dreaptă -X1 + 2x2 = 6. În acest scop, am găsit două puncte, cum ar fi punctul de intersecție cu axele de coordonate: dacă x1 = 0x2 = 3 și x2 = 0x1 = -6. adică punctul (0, 3) și (-6, 0). Pentru a izola semiplanul corespunzător în ceea ce privește coordonatele liniei de substituție construite din orice alt punct (de exemplu, originea) în partea stângă a inegalității (1). Astfel, atunci când înlocuind valorile x1 = 0 și x2 = 0 vedem că este îndeplinită condiția (0 ≤ 6). Prin urmare, gama de soluții admise ale acestei inegalități -X1 + 2x2≤6 - acea semiplanului, care include originea. Afișarea unei a doua limitare este absolut identic.

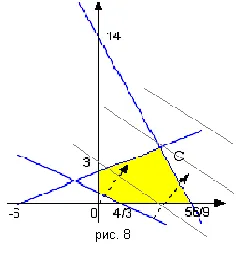
În ceea ce privește a treia constrângerile semiplanului, este situat în raport cu linia de delimitare pe de altă parte, mai degrabă decât de origine.

A patra și a cincea limita (x1≥0. X2≥0) corespund semiplanurile care se află la dreapta și ordonata pe abscisă (primul cadran al planului).

Ca rezultat, vom obține un spațiu comun pentru toate cele cinci jumătăți de avioane (in mai multe planuri) - convexe pentagon (Figura 8.).

Acum folosim gradientul funcției L (x) = 2x1 + 3x2. Acolo gradL (x) = (2. 3). Acest construct vector în figură, în numărarea de la origine (sau din orice punct al planului sau din orice punct al planurilor). Dacă punctul extremale nu este evident, să ia „firul“, care este perpendicular pe panta, și trageți peste setul de planuri în direcția funcției de gradient.

Rețineți că, în toate punctele de valoare „fire“ a funcției obiectiv în același mod (cum ar fi „nivelul liniei“ vezi, de exemplu, pe harta fizică a lumii cu imaginea de munți și adâncimi).

Este ușor de văzut că ultimul punct de contact „fire“, cu o mulțime de planuri este punctul maxim necesar al funcției L (x) (primul punct de contact - punctul minim). În exemplul nostru, punctul maxim al funcției L (x) este punctul C. Rămâne de a găsi coordonatele sale.

Din moment ce se obține prin intersecția prima și a doua linii drepte, este suficient pentru a rezolva sistemul de două ecuații cu două necunoscute

O persoană familiară cu factorii determinanți și regula lui Cramer, care decide în forma:

În cazul în care cititorul nu ia în considerare costul forței de muncă, aceasta poate fi rezolvată prin substituții sau orice altă tehnică.

Exemplul 2. Găsiți valorile extreme ale funcției