Soluția sistemului de ecuații liniare cu trei necunoscute - Matematica
Rezolva sistemul de ecuații liniare în două moduri: prin regula lui Cramer si de Gauss
1) rezolva sistem de ecuații liniare neomogene Ax = B de către Kramer
Sistemul Determinant D nu este egal cu zero. Am găsit determinanți auxiliare D1. D2. D3. în cazul în care acestea nu sunt egale cu zero, atunci nu există soluții în cazul în care, atunci un număr infinit egal de soluții
3 Sistemul de ecuații liniare cu trei necunoscute, a cărei determinant este diferit de zero, este întotdeauna consecvent și are o soluție unică, calculată după cum urmează:
A: a primit soluția:
2) rezolva sistemul de ecuații liniare neomogene Metoda Ax = B Gauss
Noi forma matricea augmentată a sistemului
Să luăm prima linie a ghidului, iar elementul = 1 A11 - pentru ghid. Folosind liniile de ghidare obține zerouri în prima coloană.
Matricea care corespunde setului de soluții ale sistemului de ecuații liniare
A: a primit soluția:
Având în vedere coordonatele vârfurilor triunghiului ABC
1) Lungimea laturii AB;
2) din laturile AB și BC și coeficienții lor unghiulare;
3) unghiul la vârf interior în radiani până la 0,01
4) AE ecuație mediană;
5) ecuație și o înălțime de lungime CD;
6) Ecuația liniei care trece prin punctul E paralel cu latura AB și un punct M de intersecție cu înălțimea CD;
7) Ecuația cercului cu centrul în punctul E, trecând prin vârful B
Construiți un anumit triunghi și toate liniile dintr-un sistem de coordonate.
1) Distanța dintre punctul A (x1, y1) și B (x2, y2), determinat prin formula
folosind care vom găsi lungimea laturii AB;
2) din laturile AB și BC și coeficienții lor unghiulare;
Ecuația liniei care trece prin cele două puncte Fiind dat un plan (x1, y1) și B (x2, y2) este de forma
Substituind în (2) coordonatele punctelor A și B, obținem ecuația laturilor AB:
Panta liniei AB KAV găsi conversia ecuația rezultată a formei de linie dreaptă ecuație cu coeficient unghiular y = kx - b.
Noi, adică, în cazul în care
În mod similar, obținem ecuația directă a soarelui și de a găsi panta.
Substituind în (2) coordonatele punctelor B și C, obținem BC partea ecuația:
Coeficientul unghiular al liniei drepte BC kVS găsi conversia ecuația rezultată pentru o ecuație linie dreaptă medie a pantei y = kx - b.
3) unghiul la vârf interior în radiani până la 0,01
Pentru a găsi unghiul nostru interior al triunghiului folosim formula:
Rețineți că ordinea calculului diferenței unghiulare a coeficienților în numărătorul fracției depinde de poziția relativă a liniilor AB și BC.
Substituind valorile calculate anterior și kVS KAV în (3), găsim:
Acum, folosind foi de calcul calculatoare de inginerie, vom obține B „1.11 rad.
4) AE ecuație mediană;
Pentru a compila ecuația mediană AE să găsim mai întâi coordonatele punctului E, care se află pe segmentul de mijloc BC
Substituind în ecuația (2) coordonatele punctelor A și E, găsim ecuația mediană:
5) ecuație și o înălțime de lungime CD;
Pentru a compila CD ecuații de înălțime utilizați linia dreaptă ecuație trece printr-un punct dat M (x0, y0) la un coeficient k unghiular predeterminat, care are forma
și starea de perpendicularitate a liniilor AB și CD, care raportul este exprimat KAB KCD = -1, unde KCD = -1 / KAB = - 3/4
Substituind în (4) în locul valorii k KSD = -3/4, și în schimb x0. Resp y0 coordonate punctul C, obținem ecuația înălțimii CD
Pentru formula de calcul pentru găsirea înălțimilor distanță folosesc CD lungimea d dintr-un anumit punct M (x0, y0) la o linie dreaptă cu ecuația Ax predeterminat + By + C = 0, care este de forma:
Substituind (5) în loc x0; coordonatele y0 punctului C, și în locul coeficienților A, B, C ale liniei AB, obținem
6) Ecuația liniei care trece prin punctul E paralel cu latura AB și un punct M de intersecție cu înălțimea CD;
Deoarece linia dreaptă necesară EF este paralelă cu linia AB, KEF = Kab = 4/3. Substituind în ecuația (4) în loc de x0; coordonate y0 punctul E, dar în schimb valoarea k KEF obține o ecuație liniară EF“.
Pentru a găsi coordonatele punctului M împreună vom rezolva linii de ecuații EF și CD.
Astfel, M (5,48; 0,64).
7) Ecuația cercului cu centrul în punctul E, trecând prin vârful B
Deoarece cercul are centrul său la un punct E (4,5, 2) și trece printr-un nod V (4, 3), raza
Canonic cerc Ecuația de rază R centrată în punctul M0 (x0, y0) este dată de
Triunghiul ABC, înălțimea CD-ului, mediana AE, FE directă. punctul M și un cerc construit în x0u sistem de coordonate în Fig.1.

Creați ecuație linie pentru fiecare punct al cărui distanță față de punctul A (2, 5), este egală cu distanța până la linia y dreaptă = 1. Construcția rezultata curbă într-un sistem de coordonate
Fie M (x, y) - punctul curent al curbei dorite. Picătură de la punctul M MB perpendicular pe linia y = 1 (Figura 2). Apoi, B (x, 1). Deoarece MA = MB.

Ecuația rezultată definește o parabolă cu vârful în punctul C (5; 1.5) și ramurile îndreptate în sus (a se vedea figura 2).
Găsiți limitele specificate:
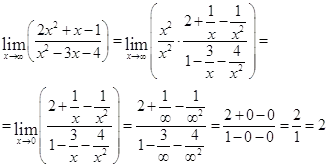
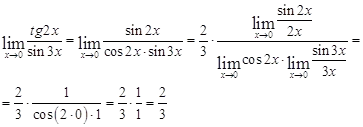
Găsiți derivat dy / dx, folosind regulile și formulele de diferențiere

Pentru a investiga funcției specificate metodele de calcul diferențial pentru a desena grafice lor.
1) Domeniul acestei funcții sunt toate valorile reale ale argumentului x, adică D (y) =, și înseamnă că funcția este continuă pe linia reală întreg și graficul ei nu are asymptotes verticale.
2) studiază funcția la intervale și Extrema monotonie. În acest scop, vom găsi derivatul său și echivala cu zero:
Rezolvarea ecuației pătratice rezultat, am ajuns la concluzia că funcția are două puncte critice ale primului x1 tip = 1, x2 = 2.
Am împărți domeniul acestor puncte în părți și să le schimbe semneze funcția derivat dezvăluie intervalele sale de monotonie și având extremele:
Valoarea x = 1.5 este abscisa punctului de inflexiune al graficului funcției, și ordonata a acestui punct:
4) Să ne determina prezența unei anumite funcții grafic asimptote. Pentru a defini asimptotă ecuația parametrului y = kx - b folosesc formulele
Astfel, graficul funcției dată nu este asimptote înclinată.
5) construim graficul
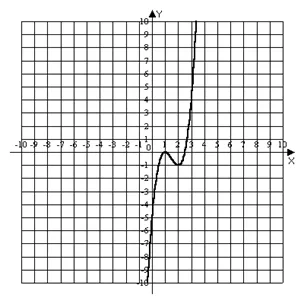
1) Domeniul acestei funcții sunt valorile argumentului x
2) Studiu privind continuitatea și punctele de discontinuitate clasificarea
Funcția dorită este continuă pretutindeni, cu excepția la punctul x = 0. Calculăm limitele sale față de la acest punct:
Deci, punctul x = 0 - punctul pauza de al doilea tip, iar linia x = 0 - asimptotă verticală.
3) studiază funcția la intervale și Extrema monotonie. În acest scop, vom găsi derivatul său și echivala cu zero:
Prin urmare, funcția nu are puncte critice de primul tip.
Deoarece y ' <0 для всех х, то функция убывает во всей области определения
4) definesc punctul de inflexiune al graficului intervalelor și convexității și concavitatea acestuia. Pentru a găsi derivata a doua a funcției date și setați-o egală cu zero:
Deci, funcția nu are puncte de inflexiune. Impartim domeniul punctului x = 1, fiecare dintre care stabilește semnul derivatei a doua:
5) Să ne determina prezența unei anumite funcții grafic asimptote. Pentru a defini asimptotă ecuația parametrului y = kx + b folosim formulele
Astfel, graficul unei funcții date are o asimptotă înclinată
6) construim graficul functiei
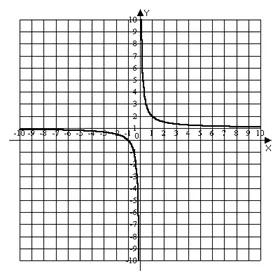
Informații despre „soluția sistemului liniar de ecuații cu trei necunoscute“
Categorie: Matematică
Numărul de caractere, inclusiv spații: 7857
Număr de mese: 3
Numărul de imagini: 7