Sistemul de bază este metoda de forțe și cerințele pentru ea

Ch. 5. Baza de calcul a teoriei sistemelor liniar deformabile. § 5.5. Teorema de reciprocitate. - S. 104-109.

2. Darkov AV Mecanica structurale: Proc. pentru școli / AV A-ing cadou, NN Shaposhnikov. - M. Executiv. Școala, 1986. - 607 p.

Ch. 5. Determinarea deplasărilor în sistemele elastice. § 5.2. Teorema-ma reciprocitate funcționează. § 5.3. Teorema de mișcări reciproce. - S. 163-168.

3. Smirnov AF Mecanica structurale. Sistemul Rod: Proc. pentru școli / AF Smirnov AV Alexandrov, BJ Lascheni-ing, NN Shaposhnikov. - M. Stroyizdat, 1981. - 512 p.

Ch. IX. Teorema de energie de bază. Proprietățile de conformitate matrici și rigiditate. § 48. Teoreme de reciprocitate. - S. 255-262.

Calculul sistemelor static nedeterminate cu forța pentru a forța de acțiune

16.1. Sistemul de bază este metoda de forțe și cerințele pentru ea

16.2. Sistemul de ecuații canonice ale metodei forțelor

16.3. coeficienții de determinare a necunoscutelor și termenii liberi ai sistemului de ecuații canonice

16.4. Determinarea forțelor interne într-o anumită construcție

16.5. validarea intermediară și finală de calcul

16.6. Exemplu de calcul al cadrului static nedeterminat cu forța

16.7. Calculul sistemelor static nedeterminate cu forța într-o formă de matrice

16.8. Exemplu de calcul cadru static nedeterminat de forțe în formă de matrice

16.9. Testați-vă cunoștințele

Luați în considerare exemplele metodei sistemelor de educație forță de bază pentru cadrele static nedeterminate (Fig. 16.1-16.8). Calculăm mai întâi gradul de redundanță a cadrelor, folosind (14.1) cu formula „contur“:

Fig. 16.1, și - = 3 x NST 3 - R6 = 3; Fig. 16,5, și - = 3 x NST 3 - 7 = 2;

Fig. 16.2, și - = 3 x NST 3 - 7 = 2; Fig. 16,6, și - = 3 x NST 3 - 4 = 5;

Fig. 16,3 și - = 2 x NST 3 - 5 = 1; Fig. 16,7, și - = 3 x NST 3 - R6 = 3;

Fig. 16,4, și - = 4 × NST 3 - 8 = 4; Fig. 16,8, și - = 2 x NST 3 - 3 = 3.

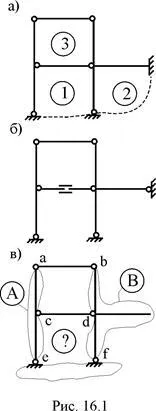
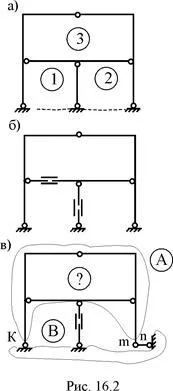
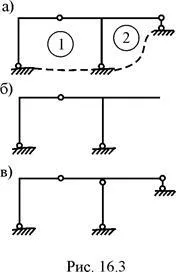
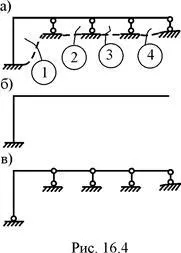
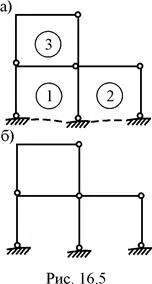
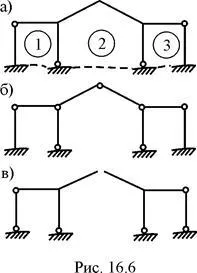
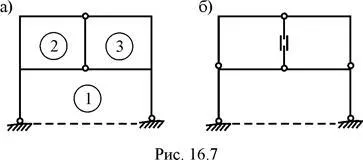
Principalele forțe metoda de sistem de cadre static nedeterminat predeterminate pot fi obținute în diferite moduri: prin eliminarea legăturilor de susținere (Figura 16.1, a; Figura 16.2, a; Figura 16.3 b, Fig 16.4, b ....) Introducerea balamale unice sau multiple cilindrice ( Figura 16.1, b ;. Fig 16.3, c ;. Fig 16.4, c ;. Figura 16.5, b ;. Figura 16.7, b) introducerea articulatiilor translatie, de obicei, în elementele care au la îmbinările lor capete cilindrice (. Figura 16.1, b ;. Figura 16.2, b, c ;. figura 16.7, b, c), eliminarea totală sau parțială a conexiunilor interne în articulația cilindrică (figura 16.8, b) se taie de-a lungul secțiunii "vii" (Fig .. . 16,6 in), iar cealaltă cu personaje, inclusiv diverse combinații ale celor de mai sus.

Având în vedere o schemă de proiectare a structurilor nedeterminate static, există mai multe variante ale sistemelor de bază ale metodei forței. Pentru a calcula versiunea acceptată care îndeplinește o serie de cerințe, printre care este cerință obligatorie imutabilitatea geometrică a sistemului de bază al metodei forței. Din această perspectivă, sistemul de bază al metodei forței, așa cum se arată în Fig. 16.1, și în fig. 16.2 în care nu poate fi utilizat pentru calcularea predeterminate cadre static nedeterminate. Sistemul de bază al metodei forței, este prezentată în Fig. 16.1, în a cărei structură o geometrica schimbătoare, deoarece este format din două discuri A și B sunt legate între ele prin trei legături paralele ab, cd, ef lungime egală. Fig. 16.2 în realizarea ilustrată o modificare instantanee în sistemul de bază al metodei forței. Într-adevăr, în acest exemplu de realizare, discul A și discul „pământ“ The interconectată cilindric balama cuplare K și mn, a cărei axă trece prin balama K.

Făcând anumite cerințe, de dorit în alegerea sistemului de bază al metodei forței ajută la reducerea timpului de calcul al structurilor static nedeterminată. Acest lucru, mai presus de toate, formarea structurii simple a sistemelor de bază de forțe, care în mod clar vizibile scheme de lucru (părți majore și minore), sunt ușor determinate de legăturile de sprijin de reacție și forțele interne. Din această perspectivă, sistemul de bază al metodei forței, așa cum se arată în Fig. 16,3 b, mai degrabă decât celălalt sistem principal (Fig. 16,3 inch) pentru același cadru.

Nu este important ca utilizat pentru calcularea sistemului de bază al metodei forțelor de diagrame ale forțelor interne este „curgeau“ asupra tuturor elementelor, de exemplu, Ne-ar fi localizate și ar avea, probabil, mai mică în valoare absolută a ordonata. îndeplinirea acestei condiții favorizează adesea introducerea îmbinărilor cilindrice în noduri este static sisteme nedeterminate (Fig. 16.4 și în Fig. 16.6, b).

Pentru structurile static nedeterminate simetrice sistemul de bază al metodei forței ar trebui să aleagă, de asemenea, o simetrică (fig. 16.6, b, c și Fig. 16.7, b).