sisteme de ecuatii liniare Rezolvarea prin adăugarea
Pentru a rezolva un sistem de ecuații liniare în două variabile, prin adăugarea, este necesară:
1) se multiplica ambele părți ale uneia sau ambelor ecuații pentru un număr, astfel încât coeficienții uneia dintre variabilele din ecuațiile devin numere opuse;
2) ecuațiile slozhitpochlennopoluchennye și găsi valoarea uneia dintre variabile;
3) Înlocuind valoarea unei variabile într-una dintre aceste ecuații și de a găsi valoarea celei de a doua variabilă.
În cazul în care acest sistem de coeficienți de unul variabile sunt numere opuse, sistemul va începe o dată soluția de la pasul 2).
Exemple. Rezolva sistemul de ecuații liniare cu două variabile, prin adăugarea.
Deoarece coeficienții y sunt inverse aditiv (-1, 1), soluția de la pasul 2). Adaugam împreună pe termen de termen al ecuației și se obține următoarea ecuație 8x = 24. Al doilea sistem de ecuații poate fi scris orice ecuație a sistemului original.
Am găsit x și înlocui valoarea din a doua ecuație.
Rezolvarea a doua ecuație: y 9 = 14, deci y = -5.
Noi facem o verificare de fond. Înlocuind valorile lui x = 3 și y = -5 în sistemul original de ecuații.
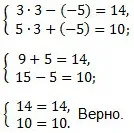
Dacă vom multiplica prima ecuație de (-2), coeficienții variabilei x vor fi numere opuse:
Punând aceste ecuații pe termen de termen.
Vom obține sistemul echivalent de ecuații, în care prima ecuație este suma celor două sistemului anterior de ecuații, iar sistemul doilea de ecuații am scrie prima ecuație a sistemului original (ecuația este scris de obicei, cu un coeficient mai mic):
Găsim provenind din prima ecuație și valoarea rezultată este substituită în al doilea.
Rezolvarea ultima ecuație și obține x = -2.
Facem coeficientul de numere opuse y variabile. În acest scop, toți membrii prima ecuatie, se înmulțește cu 5, și toți membrii a 2-a ecuației 2.
Substituind valoarea x = 4 în a doua ecuație.
3 x 4 - 5y = 27. simplifici 12 - 5y = 27, deci -5u = 15 și y = -3.