sistem de forțe plan Arbitrare

Fig. 18 prezintă un sistem de forțe care acționează în planul YOZ. Originea (punctul O) în planul de acțiune al forțelor poate fi ales în mod arbitrar. Apoi proiecțiile tuturor forțelor de pe axa OX este egală cu zero, deoarece forțele sunt perpendiculare pe axa x și momentele tuturor forțelor în jurul axelor OY si OZ sunt de asemenea zero, deoarece axa și puterea de minciună în același plan.

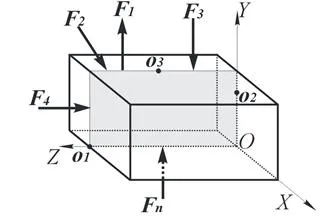
Figura 18 - Un plan arbitrar

Cursul mecanicii teoretice, se dovedește că pentru orice echilibru al sistemului plan al forțelor este pregătirea necesară și suficientă a trei ecuații independente:

Pentru un sistem arbitrar de echilibru planul de forțe este necesar și suficient ca suma proiecțiilor tuturor forțelor de pe fiecare dintre cele două axe situate în planul acestor forțe este egală cu zero, iar suma momentelor de forțe despre un punct arbitrar în planul forței este de asemenea zero.

Pentru un sistem plan, altele decât ecuațiile (1), ecuația de echilibru poate fi formulată în următoarele forme forțe:

În ecuațiile (2) punctul O1. O2 nu ar trebui să se întindă pe perpendicular pe axa OY. care se execută forțe de proiecție. De exemplu, în cazul în care punctul O1. O2 selectat pe axa OZ. apoi ultimele două ecuații din (2) urmează prima ecuație.

Pentru independența ecuațiile (3) punctul O1. o2. O3 nu ar trebui să se întindă pe o linie dreaptă în planul forțelor.

Aceste condiții de echilibru sunt larg utilizate în calculul elementelor îndoite plate (grinzi, cadre) in constructie. La calculul putem folosi oricare dintre cele trei forme de ecuațiile de echilibru (1), (2), (3), pe baza condițiilor specifice.

Sistemul de forțe paralele coplanar

Acest sistem de forțe este un caz special a discutat mai sus un sistem plan arbitrar de forțe. Este foarte comun în calculele de proiectare, deoarece forțează, de obicei, F este forța de gravitație, și anume, vertical, și, prin urmare, în paralel, de asemenea, forța.

Conform Fig. 19, toate forțele sunt paralele și se află în planul YOZ, iar acestea sunt perpendiculare pe axa OZ. Apoi proiecția tuturor forțelor pe axa OZ este egală cu zero, care corespunde ecuației de proiecție devine o identitate și de condițiile de echilibru (1) sunt două condiții:

sau folosind (2),

oi un punct (4) - un punct arbitrar din planul forțelor. În ecuațiile (5)

punctul O1 și O2 nu pot fi selectate pe o linie de forțe paralele. La rezolvarea acestor probleme punct de obicei ales pe axa OZ, care permite prima dintre ecuațiile (2) utilizate pentru verificarea calculelor.

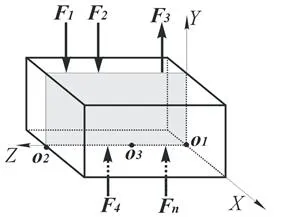
Figura 19 - Sistemul de forțe paralele coplanăr

Pentru echilibrul forțelor sistemului plat paralel, este necesar și suficient ca suma algebrică a tuturor forțelor este zero și suma momentelor forțelor relative la orice punct în planul forței este de asemenea zero.

Testați-vă cunoștințele

1. Ce este un corp rigid?

2. Ce valori și ceea ce se numește vector - scalar?

3. Care este puterea și care este dimensiunea sa?

4. Ceea ce se numește momentul forței în raport cu acest punct și care este dimensiunea sa?

5. Care este legăturile de reacție?

6. Ce sistem static echivalent de forțe?

7. Care sunt axiomele staticii ale unui corp rigid? Acestea sunt formulate?

8. Ce fel de sistem este numit forțe convergente? Cum de a determina rezultanta lor?

9. Ceea ce se numește vectorul principal al sistemului de planul de forțe?

10. Asigurați-vă condițiile de echilibru pentru un sistem plan arbitrar de forțe.

11. Asigurați-vă condițiile de echilibru pentru un sistem de forțe convergente.

12. Asigurați condițiile de echilibru pentru un sistem plană de forțe paralele.