Setul de numere raționale, cele mai mari studii portal

Setul de numere raționale

În plus față de numere raționale, există un număr de natură diferită - acestea conduc adesea la exploatarea de extragere a rădăcinii pătrate (și nu numai ei, dar noi cu voi, care nu știu). Deci, avem nevoie să cunoască mai bine cu numere noi. dar
în primul rând încercăm să organizăm cunoștințele noastre despre „vechi“, adică. e. un mod rațional, numere.

1. Unele dintre simbolurile limbajului matematic

Sunteți bine cunoscut pentru numerele naturale:
1, 2, 3, 4.
Setul de numere întregi, în general, toate notate cu litera N.
Dacă atașat la numerele naturale de 0 și toate numerele întregi negative: -1, -2, -3, -4. - veți obține un set de numere întregi. Acest set este de obicei notată cu litera Z.
În cazul în care un set de numere întregi pentru a conecta toate fracțiunile comune: .. Și așa mai departe - veți obține o mulțime de numere ratsinalnyh. Acest set este de obicei notată cu litera Q.
Orice număr întreg m poate fi scris ca o fracție. Prin urmare, afirmația că setul Q de numere raționale - este setul de numere de forma
Folosind această notație N, Z, Q, sunt de acord cu următoarele:
1. În loc de expresia „n - număr natural“, puteți scrie (a se citi: „elementul apartine setului n N»), simboluri matematice numite semn de apartenență.
2. În loc de expresia «m - număr întreg“ puteți scrie m Z.
3. În loc de expresia «r - un număr rațional“, puteți scrie r Q.
Este clar că N - o parte din Z set, și Z - o parte din Q. set Pentru o descriere a situației în matematică este, de asemenea, o notație specială:

Simbolul matematic pentru a activa indicativul de apel (un set la altul).
În general, în matematică de înregistrare x X înseamnă că X - este unul dintre elementele X. Minuta înseamnă că mulțimea A este un subset al V. Mathematics spun adesea: A - subset

Vă rugăm să rețineți: seturile în matematică sunt, de obicei, notate cu litere mari, iar elementele setului - litere minuscule.
Iar pentru un moment, nota semne accesorii (element aparține) și includerea (un set este conținut în celălalt) - diferitele, respectiv
O înregistrare așa x aparține setului X sau care A nu este o parte (subset) din setul B? Ei folosesc aceleași personaje, dar a trecut cu o bară oblică :.
Iată câteva exemple de utilizare a simbolurilor matematice introduse pentru concizie adevărate declarații matematice - de asemenea, se face referire la declarațiile ca adevărate.

2. Numerele raționale ca fracții zecimale infinite periodice

Pentru numerele raționale, așa cum am subliniat în mod repetat, sunt toate acele numere pe care le-ați operat cu succes până atunci, până când sa întâlnit cu rădăcini pătrate.
Erau numere întregi, fracții comune, zecimale.
Pentru toate aceste numere, puteți utiliza aceeași metodă de înregistrare, care acum vom discuta.
Să considerăm, de exemplu, întreg 5, fracțiunea comună și o fracție zecimală 8377. 5 întreg poate fi scris ca o fracție zecimală infinită: 5.0000. fracție zecimală 8377 pot fi, de asemenea scrisă ca o fracție zecimală infinită: 8.377000. Pentru a utiliza metoda de
„Unghiul Divizia“:

După cum puteți vedea din a doua cifre după virgulă se produce repetarea aceluiași grup de numere: 18, 18, 18. Astfel,
= 0.3181818. Pe scurt, este scris ca: 0.3 (18). grup de cifre Repetând după virgulă se numește perioada, iar foarte zecimal - fracțiunea zecimală infinită periodică.
fracție zecimală infinită periodică. Pentru a face acest lucru, în perioada de înregistrare de la 0:
5 = 5.00000. = 5 (0). Acesta este același cu numărul 8377: 8377 = 8.377000. = 8377 (0).
Pentru a păstra lucrurile în ordine, să zicem: 8377 - zecimal finit, și 8.377000. - zecimal infinit.
Astfel, numărul 5 și numărul. iar numărul 8377 poate fi scrisă sub forma unei fracții infinite zecimale periodice.
In general, orice număr rațional poate fi scrisă ca o fracție infinită zecimală periodică.

Notă. Această concluzie este utilă pentru teoria, dar nu atât de convenabil pentru practica. La urma urmei, în cazul dat o fracție zecimală finită 8377, atunci de ce
intrarea sa în formă de 8377 (0)? Prin urmare, spun de obicei: orice număr rațional poate fi scris ca o zecimală finită, sau sub forma unui infinit
clorhidric fracție zecimală periodică.
Mai sus am arătat cum o fracțiune obișnuită prezentată sub forma unei zecimale periodice infinit. Invers, orice fracție zecimală infinită periodică poate fi reprezentat ca o fracție comună. Aceasta înseamnă că orice fracție zecimală infinită periodică acolo
număr rațional.
Arătăm un exemplu de modul în care fracție zecimală infinită periodică este transformată într-o fracție ordinară.

Exemplu. Scrieți o fracție comună fracție zecimală infinită periodică: a) 1 (23); b) 1,5 (23).
Soluție a) Fie x = 1, (23), t. E. X = 1.232323.
Am multiplica x de un număr astfel încât virgula sa mutat la dreapta de exact o perioadă. Deoarece perioada conține două numere trebuie să virgulă mutat la dreapta prin două cifre, iar acest număr x este să fie înmulțit cu 100.

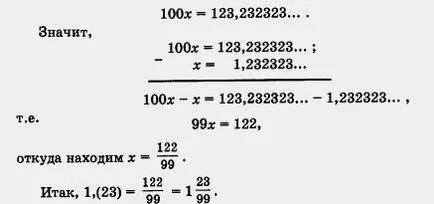
b) Set x = 1,5 (23) = 1.5232323. În primul rând, vom multiplica x cu 10 pentru a lucra în perioada obținută a început imediat după virgulă: 10x = 15.232323. Acum multiplica numărul de 10x 100 - apoi o schimbare virgulă de exact o perioadă la dreapta: 1000x - 1523.232323. avem

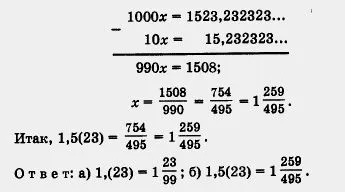
Acum am stat rezultatul principal al acestei secțiuni: Q set de numere raționale poate fi considerat ca un set de numere de forma.

unde m - este un număr întreg, n - un număr întreg sau ca o pluralitate de fracții zecimale periodice infinite.