Sensul geometric integral definit

Combinând această teoremă cu soluția III. Vedem că trapezului curbilinie, luate în considerare în problema menționată are zonă de F. și acest domeniu este exprimat prin formula

Citind această formulă drept, vom găsi

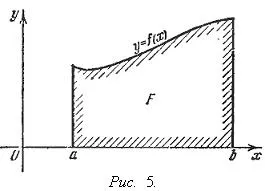
Semnificația geometrică a definit integralei. Dacă f (x) este continuă și pozitivă [a. b], integrala

Reprezintă aria unui trapez curbiliniu delimitată de liniile y = 0, x = a. x = b. y = f (x) (vezi. fig. 5).

Nu ar trebui să credem că condiția de continuitate, este necesar să se asigure că a existat o integrala definită. Integrala poate exista și funcții discontinue. Să presupunem, de exemplu, funcția f (x), definită pe intervalul [a. b], este zero la toate punctele intervalului dar un număr finit de puncte Z1. z2. ZN. Formulările pentru f (x) suma integrală # 963; .

Lăsați punctele # 958; 0. # 958; 1. # 958; n -1. incluse în definiția # 963;. puncte p coincid cu punctele de Zi. iar restul sunt diferiți de ei. Apoi, în valoare de # 963; p va doar termeni diferiți de zero. În cazul în care cele mai multe numere | f (zi) | (I = 1, 2. N) este K. atunci evident

în cazul în care este clar că # 955; → 0 va # 963; → 0. Astfel, integrala

Ea există și este zero.

Noi da acum un exemplu de funcție care nu are nici o integrală. lăsa # 966; (X) este definită pe intervalul [0, 1], după cum urmează:

Dacă noi, reprezentând suma de # 963;. pentru litera # 958; k alege un număr irațional, acesta va apărea # 963; = 0. Dacă toate # 958; k pentru a lua o rațional, veți obține # 963; = 1. Astfel, datorită simpla reducere # 955; nu poate aduce # 963; la orice număr de permanentă și integrală

În prezent, cunoaștem semnele exacte pe care le-ar dezvălui dacă sau nu funcția de Definite integrală dat, dar ne limităm la teorema de mai sus cu privire la integrabilitatea funcțiilor continue.

rezolvarea unor probleme