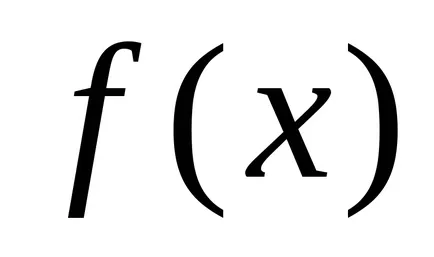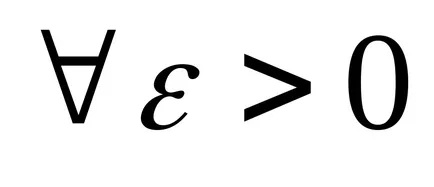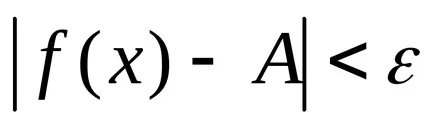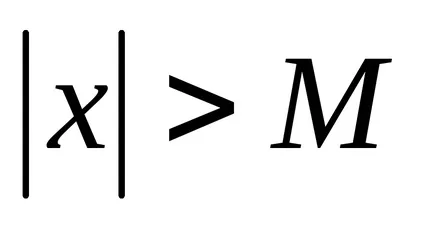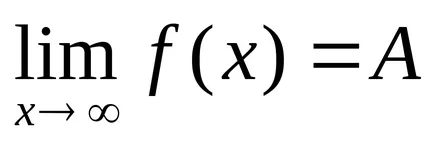secvență numerică
Luați în considerare setul de numere naturale 1, 2, 3, 4, ... ..n, ...
Să fiecare număr natural în conformitate cu unele reguli sau de drept este atribuit un număr x1 reală. x2. x3. ... xn. ... Apoi, noi spunem că mulțimea numerelor naturale este dată de secvență numerică n>.
Secvența numerică este stabilită dacă regula specificată prin care orice membru al secvenței poate fi calculată, dacă nu se cunoaște număr. Această regulă se numește secvența formuloynchlena.
De exemplu: x 2 = n
Limita unei secvențe
Numărul a este denumit limita secvenței n>, dacă pentru orice e> 0 exista Chislon (ε) astfel încât pentru vsehn> nPuteti inegalității │hp - a│<ε. Обозначают
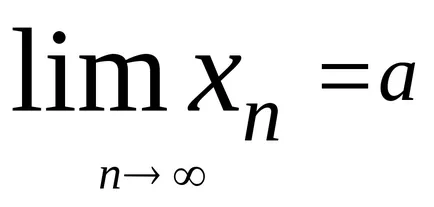
Secvența care are o limită se numește convergentă.
Inegalitatea │hn -a│<ε равносильно неравенству а – ε <хn Numărul A se numește limita a secvenței, în cazul în care pentru orice e> 0 există Chislon (ε), că toți termenii secvenței cu nomeramin> Npopadut în gruparea e - vecinătatea unui. În afara acestui cartier sau nu acolo xn puncte. sau există un număr finit de ele. Teorema 1. În cazul în care secvența are o limită, atunci este unic. Să secvența are două limite diferite și a și b. Luați în considerare un cartier de puncte ibtakoy cantități mici, care nu se intersectează. Noi folosim a doua determinare ulterioară a-limită succesive. Deoarece numărul și secvența limita, atunci există un punct de cartier și că toți membrii, cu excepția secvenței poate fi dintr-un număr finit în cădere ε - vecinătate a unui. Deoarece limita chislobyavlyaetsya a unei secvențe, toți termenii secvenței, cu excepția doar un număr finit de ele se încadrează în ε - tochkib cartier. Astfel, toți membrii setului au fost infinit în vecinătatea a două puncte diferite, care nu pot fi. O contradicție. În consecință, numai limita, iar teorema este adevărată. suma algebrică întindere a unui număr finit de secvențe este egală cu suma algebrică a termenilor secvențelor în afara cazului în care există aceste din urmă limite. Limita de produs a unui număr finit de secvențe este egal cu produsul factorilor de secvențe în afara cazului în care există aceste din urmă limite. Limita de secvențe private, este un privat în afara numărătorul și numitorul, în cazul în care există aceste limite și limita numitorul secvenței este diferită de zero.Proprietățile de bază ale limitelor
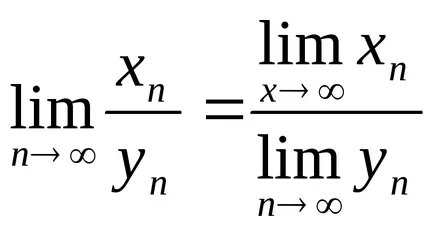
Să ne dovedesc, de exemplu, prima declarație.
Să presupunem că există două secvențe de n> și n> și suma n + yn>. Pentru a dovedi că
Noi folosim definiția limitei secvenței.
lăsa
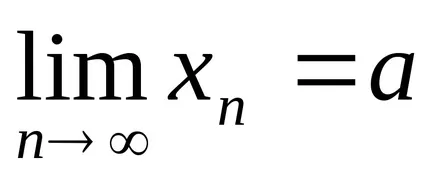
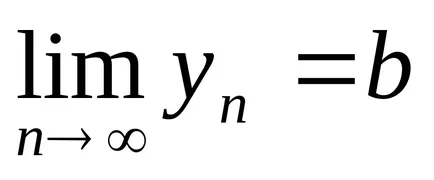
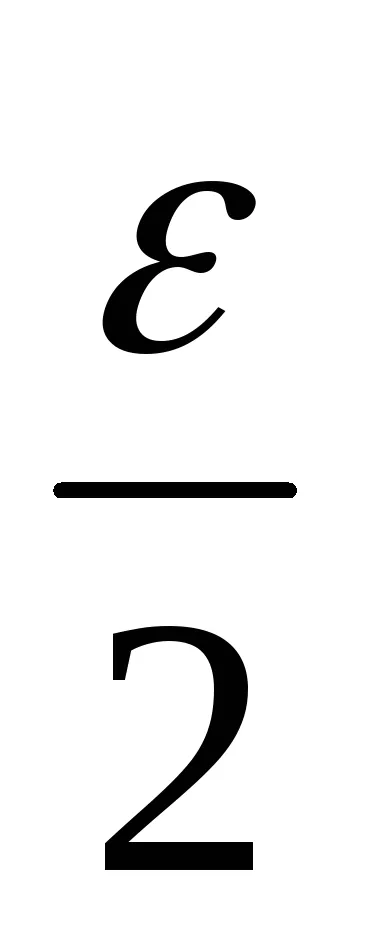
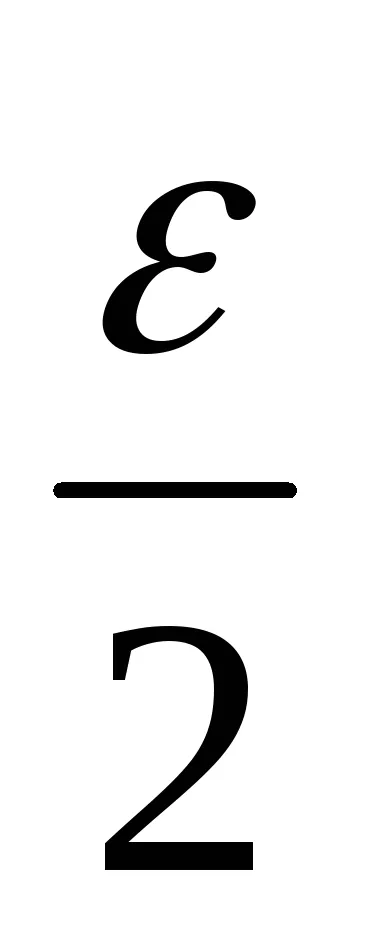
Forma modulul diferenței dintre numărul de ordine al sumei și nchlenom (a + b) și utilizați pentru proprietățile modulului și inegalitățile de mai sus.
│ (xn -yn) - (a + b) │ = │ (xn -a) + (yn -b) │<│xn -a│+│yn -b│<
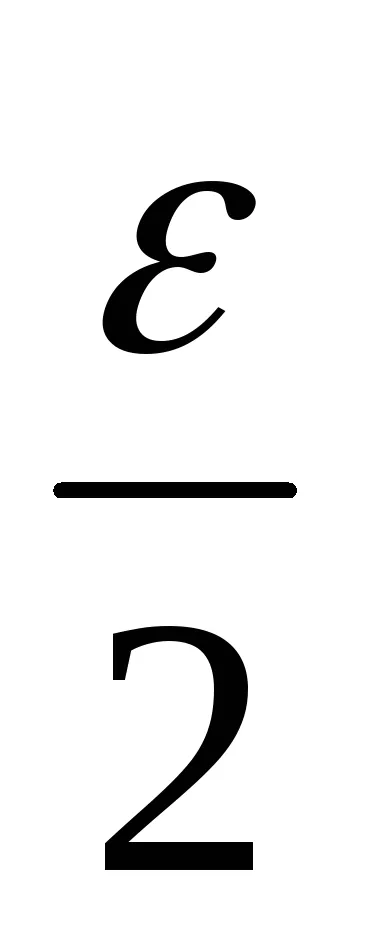
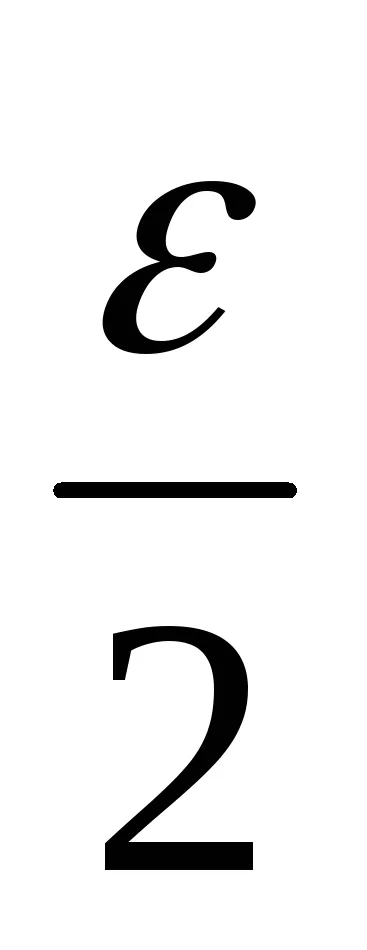
Apoi, prin definiție limită de secvență, declarația în cantitatea potrivită de secvență.
Afirmațiile rămase sunt dovedite în mod similar.
Fie funcția
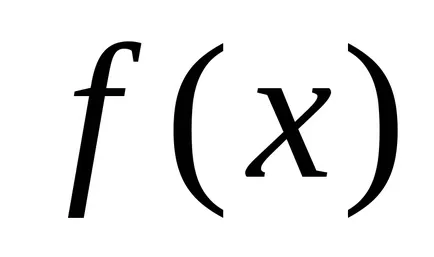
Definiție 1. Numărul A se numește funcția limită
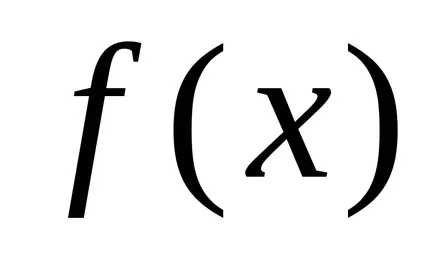
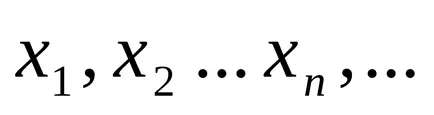
Consultați-l în acest fel:
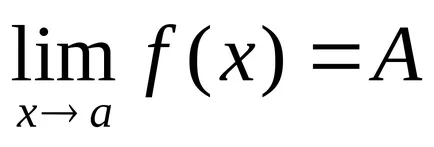
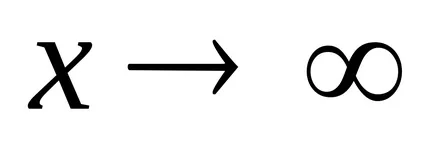
Dacă secvența de valori ale funcției tinde să
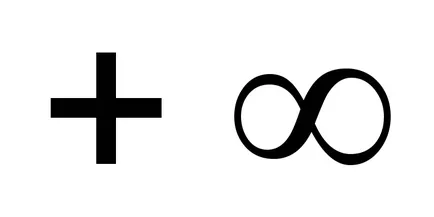

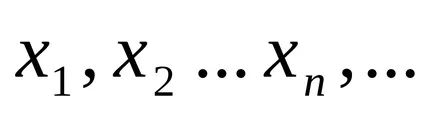
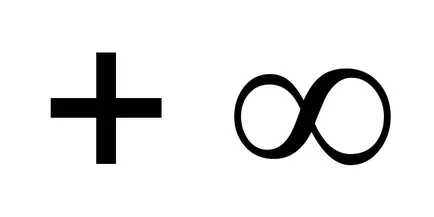

Consultați-l în acest fel:
limita de
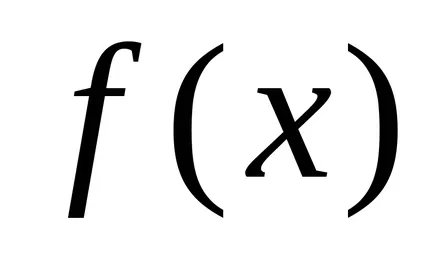
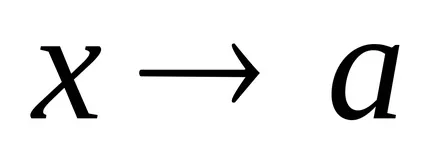
Definiție 2. Numărul A se numește funcția limită
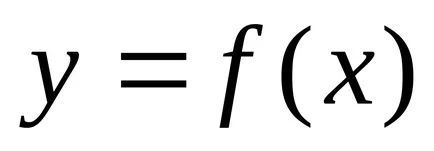
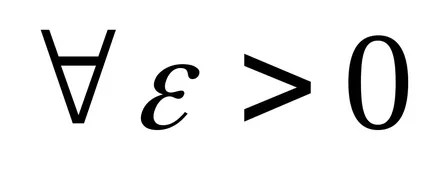
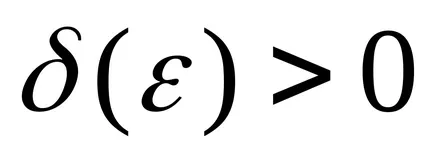
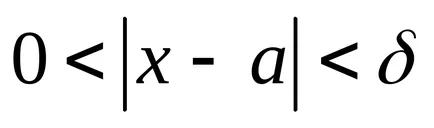
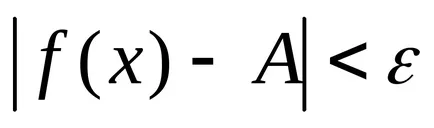
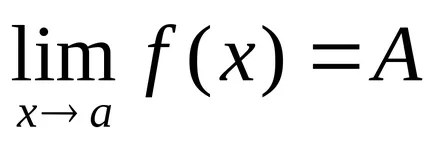
Este ușor de dovedit că ambele definiții sunt echivalente cu funcția de limită.
Grăitor definirea limitei poate fi reprezentat după cum urmează:
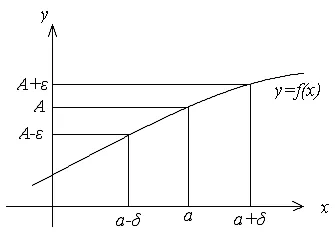
Odată ce argumentul x se încadrează în valorile


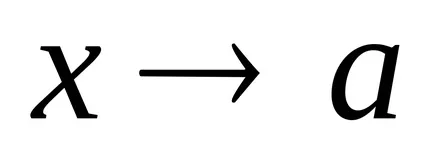
în mod opțional, o funcție a fost determinată la punctul a;


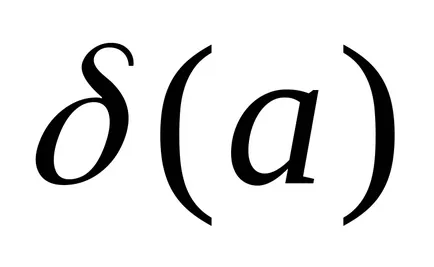
Definiție 3. Numărul A este funcția limită