regresie simbolică
De învățare automată.
regresie Simbolic - metoda de construire a modelelor de regresie prin încercarea de diferite superpoziții arbitrare de funcții ale unui anumit set. Componența funcții în același timp se numește un „program“, și algoritmi de optimizare stocastice pentru a construi un astfel de superpoziție se numește programare genetică.
Declarația problemei
Problema găsirii optime structura modelului de regresie mai multe variabile libere urmează. Set de prelevare de probe - multe _1, \ ldots, \ mathbf_N | \ mathbf \ în \ R ^ M \> „> valori ale variabilelor libere și multe din valorile variabilei dependente corespunzătoare reprezintă ambele seturi ca set de date de intrare ..
De asemenea, având în vedere un set de "funcții > netede parametrice, \ cdot, \ cdot, \ ldots, \ cdot)" >. Primul argument al funcției - parametrii vector rând „> ulterioare -.. Variabilele din setul de numere reale, privite ca elemente ale vectorului variabilelor libere Luați în considerare o superpoziție format din nu mai mult de funcții Acest superpoziție stabilește modelul de regresie prin parametri, \ mathbf)“ / >. Modelul de regresie în funcție de vectorul variabilelor libere „> și vectorul parametrilor“ >. Vector \ in \ ^ R W "> este format din vectori conectați parametri ai funcției, adică = \ mathbf_1 \ vdots \ mathbf_2 \ vdots \ ldots \ vdots \ mathbf_r" >, unde - vectori semn de aderare. Notăm „> - setul de suprapunerilor, generat de setul inductiv.
Trebuie să selectați un model care oferă maximul specificat funcțional | D) „> Această funcțională definește funcția obiectiv)“ >, care este utilizat în calcule.
Procedura de căutare a modelului optim
Căutare model optim vine pe o varietate de modele generate la fiecare iterație a algoritmului. Înainte de utilizare a algoritmului dat un set de date măsurate și setul de funcții netede. Setați setul inițial de modele concurente, în cazul în care fiecare model este o suprapunere de funcții \> _ ^ „>. În cazul în care nu există nici un set inițial de modele, este generat aleator. În plus, succesiunea etapelor de mai jos.
1. Metoda de gradient conjugat (sau alte setări metodă) sunt funcții de penalizare minimizate) „> pentru fiecare model. Opțiunile sunt gasite ^ \ m_i“ > și valoarea calculată a funcției de penalizare a fiecărui model.
2. Setați următoarele reguli pentru construirea de modele de instrumente derivate. Fiecare model este construit modelul derivat. În funcție selectate aleatoriu „>. Selectați orice model de“ > și funcția sa arbitrară „>. Modelul este generat de funcția de modelare prin înlocuirea“ > cu argumentele sale funcția „> cu argumentele.
3. Cu un model prestabilit de probabilitate a fiecărui supus să se schimbe. Modelul variabil -taya selectat funcția, și legea de distribuție a probabilității set de selectare a funcției. O multitudine de funcții selectate aleatoriu, și înlocuiește funcția. Hyperparameters "> Această funcție este definită ca)" >. Parametrii acestei funcții vectoriale _ „> este egal cu zero sau atribuite cu sarcina.
4. La selectarea unui model dintr-un set unitar de modele părinte și copil, în conformitate cu criteriul) „> pentru a alege cele mai bune pentru a fi utilizate în iterații ulterioare.
Algoritmul este oprit atunci când eroarea nu depășește un predeterminat, sau atunci când un anumit număr de ori.
Un exemplu de model de construcție
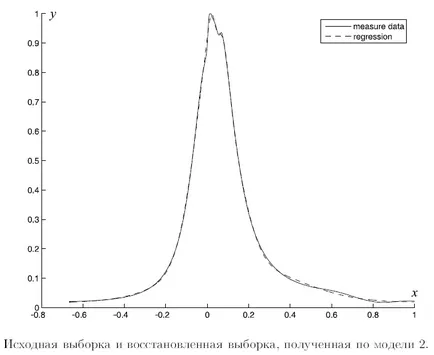
Ceea ce urmează descrie un exemplu de construcție a unui model de regresie simbolic. Figura 1. Curba solidă arată datele brute, linia punctată arată valorile modelului de regresie. Abscisa indică valoarea unei variabile libere, iar axa ordonatei - valoarea variabilei dependente. Eșantionul reprezentat de această curbă cuprinde patru mii de probe. Experții s-au dat un set de funcții de bază ale elementelor din care sunt generate de modelul de regresie. Lista de funcții este dată în tabel. O mulțime de modelul inițial de aproximare a fost, de asemenea, dat de experți.

Alegerea modelelor produse de la mai mult de o mie de modele generate. Tabelul 2 prezintă cele trei modele obținute prin algoritmul. Calitatea modelelor a fost evaluată de erori și numărul de parametri din vectorul parametrului „> Eroare -. Rms eroare relativă
eroare - eroarea relativă maximă

Linia „descriere“ Tabelul 2 prezintă structura modelului într-un copac. Ca un exemplu, ia în considerare modelul 2. Modelul este compus dintr-o suprapunere de opt funcții. Funcțiile și adăugarea și multiplicarea sunt primul argument parametri vectori; , Și _4, \ cdot) ">. Funcții \ sigma_i> \ mbox \ stânga (> \ dreapta)" > sunt parametrii vectori _I = \ Langle \ lambda_i, \ mu_i, \ sigma_i, „>, și funcția acesta are un vector parametru _4 = \ Langle.
Modelul poate fi rescrisă ca, \ x) = l (\ mathbf_4, x) ^ \ ori \ stânga (x + \ sum_³h (\ mathbf_i „> unde = \ mathbf_1 \ vdots \ mathbf_2 \ vdots \ mathbf_3 \ vdots \ mathbf_4 „> modele Blog Vizualizare .: