Recursivitatea în Pascal, funcții și proceduri recursive

În cazul în care corpul funcției întâlnește provocarea acestei funcții foarte. atunci acest lucru este recursivitate.

Recursiv în Pascal poate avea atât funcțiile și procedurile.

De fapt, recurențe poate fi infinit. Dar, la fel ca orice alt algoritm, acesta trebuie să returneze un rezultat după un anumit număr definit de operații.

Prin urmare, este important: La fiecare etapă a procedurii sau a corpului funcției recursive necesar o schimbare în parametrul funcției, sau existența condițiilor în care aceasta nu se mai în sine nu va provoca!

Luați în considerare un simplu exemplu de utilizare a unei proceduri recursiv:

Exemplu: numerele de secvență de imprimare în ob.patno-comandă utilizând o procedură de apel recursiv. nappimep:
rând (5) = 5 4 3 2 1
Din starea problemei este clar că starea de finalizare a recursie este un argument funcție în sine, care ar trebui să fie redusă cu o până când este> = 1.

Procedura rând (n: integer); începe dacă n> = 1 apoi începe scriere (n, ''); (N-1) sfârșitul rând; se încheie; începe rând (10); end.

Acum, ia în considerare un exemplu mai complex de utilizare recursie în Pascal.

Exemplu: Scrieți o procedură recursiv care afișează numerele trecut ca un număr de parametru real, în ordine inversă.

De exemplu: în cazul în care funcția a trecut, inclusiv 3078. trebuie să se întoarcă în cele din urmă 8703
Utilizați operațiuni Mod si div

Procedura inversă (n: integer); începe scriere (mod n 10); if (n div 10) <> 0 apoi inversa (n div 10) de capăt; începe writeln; reverse (3078); end.

Recursivitate: secvență de imprimare folosind recursivitate:
25,23,21,19,17 ... 0

Acum, să vedem cum recurență este utilizat în calculul factorial în Pascal.

Exemplu: Faceti o funcție recursivă pentru a calcula factorialul

Sugestie:
2! = 2 * 1 = 2
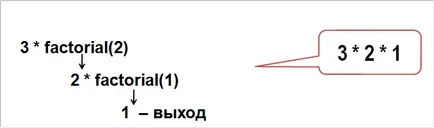
3! = 3 * 2 * 1 = 6
Derivarea formula a! = A * ((a-1)!)

var x: integer; Funcția de fapt (a: integer): integer; începe dacă (a<=1) then a:=1 else a:=a*(fact(a-1)); fact:=a; end; begin writeln('Число?'); readln(x); writeln(fact(x)); end.

Recursivitate: Scrieți o funcție recursivă sumTo (n). că, pentru un anumit n calculează suma numerelor de la 1 la n. de exemplu:
sumTo (1) = 1
sumTo (2) = 2 + 1 = 3
sumTo (3) = 3 + 2 + 1 = 6
.

Recursivitatea. Scrieti o functie recursiva de determinare a gradului.

var x, y: integer; Funcția Stepen (a, b: integer): integer; var. începe. se încheie; începe writeln ( 'număr'); readln (x); writeln ( 'măsura'); readln (y); writeln (Stepen (x, y)); end.

Recursivitate: Este necesar pentru a simula funcționarea unui pentru buclă. Pe de fiecare dată cuvântul „salut“ și valoarea contorului. Pentru a face acest lucru, utilizați un contor pas variabil, care urmează să fie pus în aplicare ca parametru procedură. A doua opțiune - numărul total de etape (numărul de iterații ale buclei).

Recursivitate: Găsiți GCD de Euclid. Utilizați o procedură recursiv.

Pentru numerele 3430 și 1365:

restul de divizare 3430-1365

3430 mod 1365 = 700

reziduul nu este zero, pentru a repeta aceeași acțiune, înlocuind primul număr al doilea, și în locul al doilea - reziduul

1365 mod 700 = 665

reziduu de asemenea la zero, astfel încât o altă divizare

700 mod 665 = 35

reziduu de asemenea la zero, astfel încât o altă divizare

Recursivitate: Print primele 10 numere Fibonacci (până la 21), folosind un proces recursiv cu doi parametri.
Rezultatul ar trebui să fie: 1 2 3 5 8 13 21 34 55 89
Cod complet: