Raporturile în triunghi, matematica

228. În acest capitol, vom fi în principal înțeleasă sub denumirea segmentelor AB, AC și așa mai departe. D. Exprimându-și numerele lor.

Știm (p. 226) că, dacă ni se oferă un geometric două segmente de susținere a și b, atunci putem construi o medie proporțională între ele. Să presupunem acum că segmentele nu sunt numere și geometric, adică. E. Sub a și b, ne referim la numărul de exprimare 2 segmente de date. Apoi găsește intervalul mediu va fi redus proporțional cu determinarea proporțiilor x a / x = x / b, unde a, b x forme și. Din această proporție, avem:

229. Să presupunem că avem un triunghi dreptunghic ABC (iunie 224).

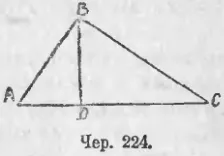
Picătură din partea de sus a unghi drept (linia ∠B) lui BD perpendicular pe ipotenuzei AC. . Apoi, de la 225 știm:

1) AC / AB = AB / AD 2) AC / BC = BC / DC.

Prin urmare, obținem:

2 AB = AC · AD si BC 2 = AC · DC.

Infasurat pe părțile laterale ale egalității, obținem:

AB + BC 2 2 = AC · AD + AC · DC = AC (AD + DC).

t. e. pătratul de exprimare a ipotenuzei este egal cu suma pătratelor numerelor care exprimă picioarele unui triunghi dreptunghic.

Pentru zicem scurt, pătrat ipotenuzei unui triunghi dreptunghic este egal cu suma pătratelor celorlalte două laturi.

Dacă vom da formula care rezultă, interpretarea geometrică, obținem teorema lui Pitagora familiară (161 n.):

pătrat construit pe ipotenuza unui triunghi dreptunghic, este egal cu suma pătratelor construite pe Catete.

Din ecuația AB 2 + BC 2 = AC 2 este uneori necesar pentru a găsi piciorul unui triunghi dreptunghic, ipotenuza și pe de altă parte un picior. Se obține, de ex.:

AB 2 = AC 2 - BC 2, și urme.

230. Raportul numeric obținut între laturile unui triunghi dreptunghic ne permite să rezolve mai multe probleme de calcul. Să ne rezolva unele dintre ele:

1. Se calculează o zonă triunghi echilateral pe această parte a acestuia.

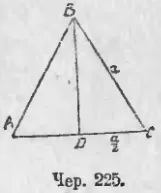
Să ΔABC (Iun. 225) este echilateral, iar fiecare parte a acestora este exprimată prin numărul unui (AB = BC = AC = a). Pentru a calcula aria acestui triunghi trebuie să-l învețe mai întâi înălțime BD, pe care o numim prin h. Știm că într-un triunghi echilateral împarte înălțimea bazei BD AC în jumătate, t. E. AD = DC = a / 2. Prin urmare, dintr-un triunghi-dreapta DBC au:

2 BD = BC 2 - DC 2

h 2 = a 2 - a = 2/4 3a ​​2/4 (efectua scădere).

(Factor de transfer de sub rădăcină).

În consecință, la apelarea numărului care exprimă zona noastră triunghiulară, prin Q și știind că zona ΔABC = (AC · BD) / 2, găsim:

Ne putem uita la această formulă, ca una dintre modalitățile de a măsura suprafața unui triunghi echilateral: este necesar să se măsoare partea sa în unități liniare, construi numere ce se găsește în piață, înmulțiți numărul respectiv √3 și împărțit în 4 - obține expresia în zona pătrat (respectiv) unități.
2. Laturile triunghiului sunt 10, 17 și 21 Ling. este unul. Se calculează suprafața sa.

Omite înălțimea h în triunghiul nostru (cher 226.) Pe partea de mare - aceasta va avea loc cu siguranță în interiorul triunghiului ca triunghiul unghi obtuz poate fi setat doar pe latura mare. Apoi latura mare = 21, împărțită în două segmente, dintre care una este notată prin x (a se vedea desenul.) - atunci celălalt = 21 - x. Obținem două triunghiuri drepte, din care avem:

h 2 = 10 2 - x 2 și 2 h = 17 2 - (21 - x) 2

Deoarece laturile din stânga ale acestor ecuații sunt aceleași,

10 februarie - 2 x 2 = 17 - (21 - x) 2

Urmați pașii de mai obținem:

Brumărel 2 - x 2 = 289-441 + 42x - x 2

Simplificând această ecuație, găsim:

Apoi, din ecuația h 2 = 10 2 - x 2. obține:

h 2 = 10 2 - 6 2 = 64

Apoi, există suprafața necesară:

Q = (21 · 8) / 2 quad. este unul. = 84 quad. este unul.

3. Este posibil pentru a rezolva o problemă comună:

cum să calculeze aria unui triunghi pe partea lui?

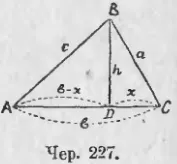
triunghi ABC Presupunem că partea sunt exprimate prin numere BC = a, AC = b și AB = c (Iun. 227). Presupunem că AC are o petrecere mare; apoi du-te în interiorul înălțimea BD ΔABC. Noi spunem: BD = h, DC = x și apoi AD = b - x.

De la ΔBDC avem: h 2 = a 2 - x 2.

De la ΔABD au: h 2 = c 2 - (b - x) 2,

dintr-o 2 - x 2 = c 2 - (b - x) 2.

Rezolvarea acestei ecuații, obținem succesiv:

2BX = a 2 + b 2 - c 2 și x = (a 2 + b 2 - c 2) / 2b.

Mai mult, înlocuind această expresie în ecuația h = a 2 2 - x 2. find

(Acesta din urmă este scris pe baza faptului că 4a numărătorul 2 b 2 - (a 2 + b 2 - c 2) 2 pot fi privite ca pătrate de egalitate, care se descompun prin produsul suma diferenței).

Această formulă este transformată, prin introducerea perimetrului unui triunghi, notat prin 2p, r. F.

Scăzând la 2c din ambele părți ale ecuației, obținem:

a + b + c - 2c = 2p - 2c sau a + b - c = 2 (p - c):

c + a - b = 2 (p - b) și c - a + b = 2 (p - a).

(P exprimă triunghi semiperimetrul).
Etoyu formulă poate fi utilizată pentru a calcula aria unui triunghi pe trei laturi.

1. Baza unui triunghi isoscel este de 10 dm. și zona = 60 sq. dm. Găsiți (calcula) perimetrul.
2. laturile paralele ale unui trapez isoscel sunt egale cu 16 și 40 dm. și fiecare dintre laturile neparalele = 37 dm. Se calculează suprafața sa.
3. Laturile trapezului sunt egale cu paralele 15 și 36 dm. și nonparallel 13 și 20 dm. Calculați zona lor.
4. Partea de rombul și ei mai mică diagonală aceeași. Găsiți formula pentru măsurarea suprafeței de model de diamant pe o parte.
5. Picioare ale triunghiului dreptunghic sunt egale, respectiv, 6 și 8 inch. Găsiți lungimea ipotenuzei, încheiat între bisectoarea unghiul direct al triunghiului și altitudinea trase din vârful unghiului drept.
6. Bisector triunghi ipotenuza unui unghi drept împarte segmentul în 2 egal cu lin respectiv. este unul. Se calculează suprafața sa.
7. Găsiți partea ta de pătrat, este egală cu un triunghi isoscel, dintre care laturile = 12 ½ Ling. este unul. iar înălțimea se referă la baza, ca 2. 3.
8. Părțile laterale ale paralelogramului sunt egale cu a și b și unul dintre unghiurile = 45 °. Găsiți o formulă pentru zona sa.
9. Unghi paralelogramului = 30 °; exprima aria prin latura sa (a și b).

232. În Sec. 229 am găsit relația dintre laturile unui triunghi dreptunghic. Puteți găsi o relație similară cu părțile (cu adăugarea unui alt segment), triunghi oblică-unghi.

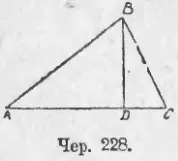
Să presupunem că avem un prim ΔABC (iunie 228), astfel încât ∠A a fost ascuțit. Vom încerca să găsească o expresie pentru pătratul BC, care se află în unghiul ascuțit (la fel ca în Sec. 229 expresie găsite pentru pătratul ipotenuzei).

Construirea unui BD ⊥ AC, obținem de la un triunghi dreptunghic BDC:

BC 2 = BD 2 + 2 DC

Înlocuiți BD2, definind-o de la ABD, în cazul în care avem:

2 BD = AB 2 - 2 AD

și înlocuiți segmentul de curent continuu prin intermediul AC - AD (este clar că DC = AC - AD). Atunci obținem:

BC 2 = AB 2 - AD 2 + (AC - AD) = AB 2 2 - AD 2 + AC 2 - 2AC · AD + 2 AD

Urmați termeni similari, vom găsi:

BC 2 = AB 2 + AC 2 - 2AC · AD.

Această formulă are următorul cuprins: partea pătrată a triunghiului, care se află pe un unghi ascuțit, egal cu suma pătratelor sale alte două laturi minus de două ori produsul uneia dintre aceste părți din partea superioară a segmentului său dintr-un unghi ascuțit față de înălțimea.

233. Acum, să ∠A și ΔABC (iunie 229) tocit. Am găsit o expresie pentru pătratul BC, situată pe un unghi obtuz.

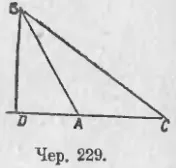
Prin construirea înălțimii BD - se află acum oarecum diferit: 228 ∠A în cazul în care punctele ascuțite C și D sunt situate pe o parte a A, ca aici, în cazul în care ∠A puncte boante C și D vor fi amplasate pe diferite părți ale unei rectangulare A. Apoi, ΔBDC obține:

BC 2 = BD 2 + 2 DC

Putem înlocui BD2, definind-o de la un ΔBDA dreptunghiular:

2 BD = AB 2 - 2 AD

iar segmentul DC = AC + AD, care este evidentă. Substituind, obținem:

BC 2 = AB 2 - AD 2 + (AC + AD) = AB 2 2 - AD 2 + AC 2 + 2AC · AD + AD 2

Urmați termeni similari, vom găsi:

BC 2 2 = AB + AC 2 + 2AC · AD,

t. e. partea pătrată a triunghiului, care se află în unghiul obtuz, egal cu suma pătratelor sale alte două laturi, plus de două ori produsul uneia dintre ele pe tăiat-o din partea de sus a unghiului obtuz la înălțimea.
Această ecuație, precum și formula și p. 232, permit o interpretare geometrică, care este ușor de găsit.

234. Utilizarea revendicărilor proprietăți. 229, 232, 233, putem, dacă ne sunt date latură a triunghiului în numere, a se vedea dacă acesta are un triunghi drept sau unghi obtuz.

unghi drept sau obtuz într-un triunghi pot fi plasate numai împotriva cea mai mare parte, ceea ce este unghiul împotriva ei, este ușor de învățat: unghiul este ascuțit, directă, sau prost, în funcție de dacă pătratul latura mare mai mică, egală sau mai mare decât suma pătratelor celorlalte două laturi .

Aflați dacă există o directă sau un unghi obtuz în următoarele triunghiuri definite de către părțile lor:

1) 15 dm. 13 dm. și 14 dm.; 2) 20, 29 și 21; 3) 11, 8 și 13; 4) 7, 11 și 15.

235. Să avem un ABCD paralelogram (cher 230.); construi diagonalele sale AC și BD și înălțimea BK ⊥ AD și CL ⊥ AD.

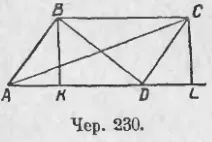
Apoi, dacă ∠A (∠BAD) ascuțit ∠D (∠ADC) neapărat prost (deoarece suma lor = 2d). De la ΔABD, în cazul în care se simt ∠A ascuțite, avem:

2 BD = AB 2 + AD 2 - 2AD · AK,

și de la ΔACD, în cazul în care ∠D tocit, avem:

AC 2 = AD 2 + 2 CD + 2AD · DL.

Înlocuiți ultimul segment al formulei AD egal cu segmentul BC și DL egal cu AK (DL = AK, pentru ΔABK = ΔDCL, așa cum este ușor de văzut). Atunci obținem:

AC2 = BC2 + CD2 + 2AD · AK.

Adăugarea de expresie pentru BD2 cu ultima expresie pentru AC 2. Găsiți:

2 BD + AC = AB 2 2 2 + AD + BC 2 + CD 2

ca membrii -2AD · AK și + 2AD · AK se anulează reciproc. Putem citi ecuația rezultată:

Suma pătratelor diagonalele unui paralelogram este egală cu suma pătratelor laturile sale.

236. Calculul mediana și bisectoarea unui triunghi pe laturile sale. triunghi ABC Presupunem că (Iun. 231) construit mediana BM (m. E. AM = MC). Știind partea ΔABC: BC = a, AC = b și AB = c, pentru a calcula valoarea mediană a BM.

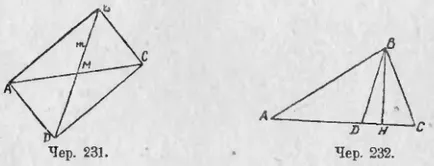
BM va continua să concedieze și se taie MD = BM. Combinarea D cu A și D cu C, obținem ABCD paralelogram (figura ușoară deoarece ΔAMD = ΔBMC și ΔAMB = ΔDMC).

Apelarea mediană BM prin m, vom obține BD = 2m, iar apoi, folosind alineatul precedent .:

237. Calcularea razei cercului circumscris despre triunghiul. Hai despre ΔABC (Iun. 233) descrie un cerc O. construct diametrul cercului BD, BH coardă AD și înălțimea triunghiului.

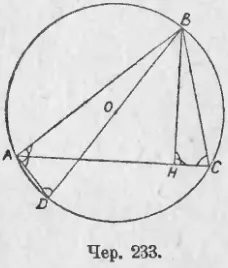
ΔBCH (∠A = ∠H = d - Un unghi drept, deoarece este înscris pe baza diametrului și BD ∠D = ∠C, cum ar fi inscripționată, bazat pe un arc AB). Prin urmare, avem:

sau prin apelarea prin raza OB R, BH prin înălțimea h și laturile AB și BC ca mai înainte, și c, respectiv, prin:

dar zona ΔABC = Q = bh / 2, unde h = 2Q / b.

Prin urmare, R = (abc) / (4Q).

Putem (p. 230 jos. 3) se calculează aria unui triunghi Q pe laturile sale. Din aceasta putem calcula R pe trei laturi ale triunghiului.

238. Calcularea razei cercului înscris în triunghiul. Inscriu △ ABC, laturile care sunt (Iun. 234), gama de O. să se conecteze la centrul O al vârfurile triunghiului și atinge punctele D, E și laturile F ale cercului, descoperim că raza OD cerc, OE și OF sunt înălțimea triunghiului BOC, COA și AOB.

Apelarea prin înscris raza cercului r, avem: