Quest-uri - matematica GDZ, algebra, geometrie, clasa 2-11
30.1 Determinați care semnul este derivata y = f (x) la puncte cu abscise a, b, c, d, dacă funcția de planificare este prezentat în desene:
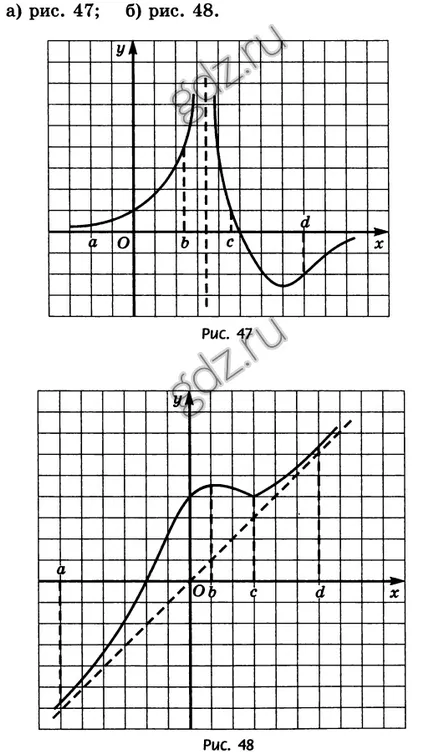
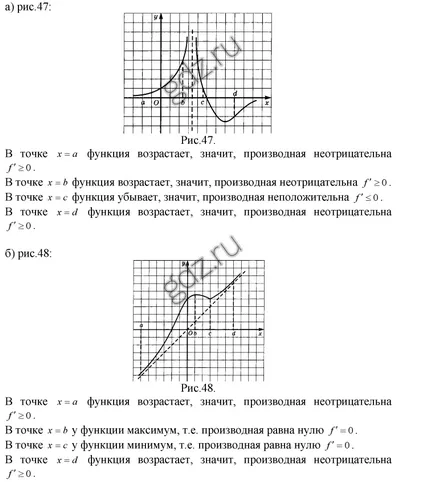
30.2 Determinarea intervalelor de creștere și descreștere a funcției a cărei grafic este prezentată mai jos:
30.3 derivat Programat ilustrat în figuri, definesc funcția decalaje y = f (x) crește, și la care - scăderi:
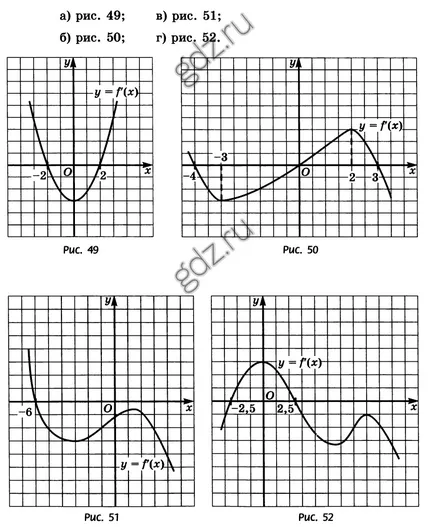
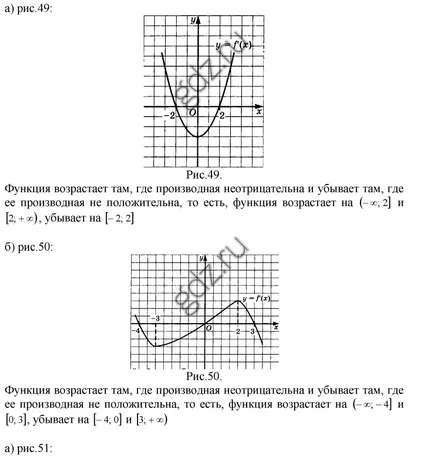
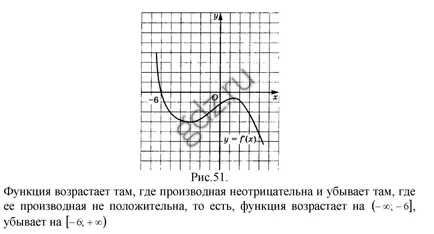
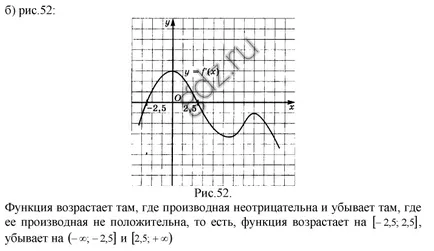
30.4 În unele dintre aceste decalaje funcționa y = f (x) scade, dacă graficul derivatului său este prezentat în Figura 50:
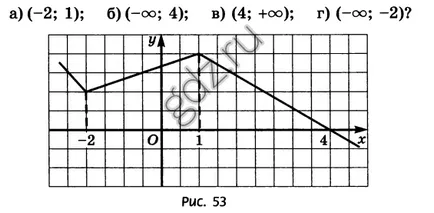

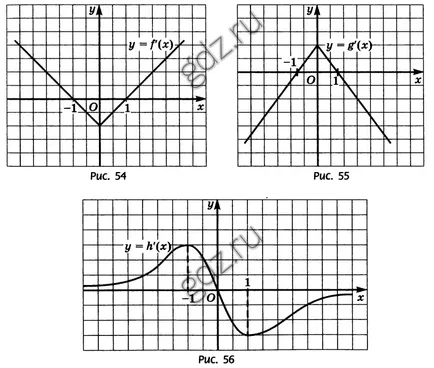
30.5 Se determină care dintre funcțiile pentru y = f (x), y = g (x), y = h (x) intervalul [-1; 1] este o perioadă de creștere, în cazul în Figurile 54-56 sunt grafice derivate din aceste funcții:
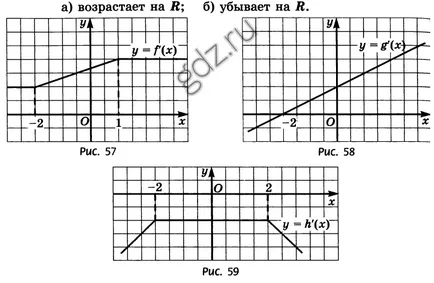
30.6 Figurile 57-59 sunt grafice derivate funcții y = f (x), y = g (x), y = h (x). Se determină care funcția y = f (x), y = g (x), y = h (x):
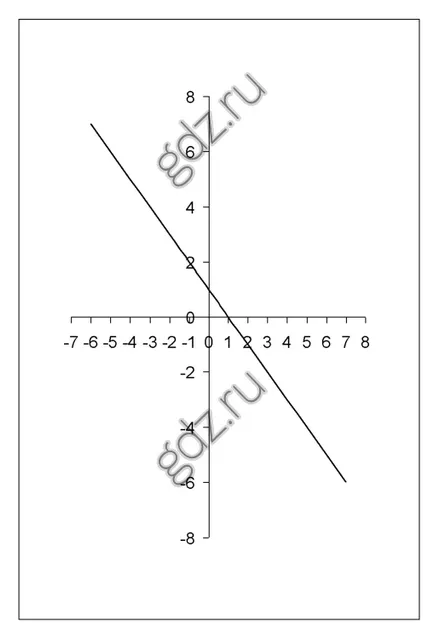
30.7 desena un grafic schiță a derivatului funcției y = f (x), în cazul în care se știe că funcția y = f (x) crește de-a lungul liniei (-∞; 1] și scade de-a lungul liniei [1 + ∞).
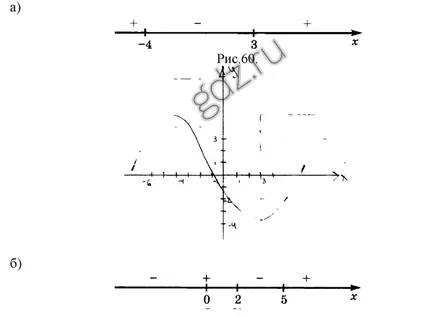
30.8 desena un grafic schiță a unei funcții y = f (x), în cazul în care semnul intervalelor constante derivate f „(x) este prezentat într-un model predeterminat:

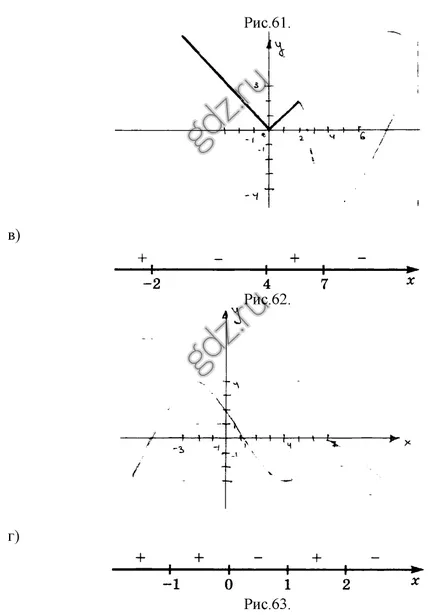
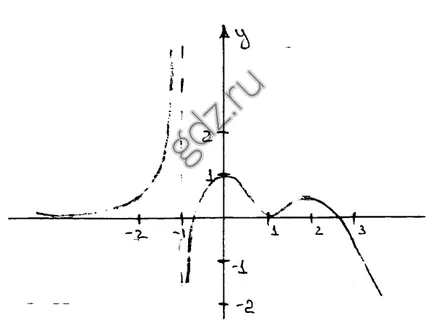
30,9 Arătați că funcția dată este în creștere:

30.10 Arătați că funcția dată scade:
30.11 Dovedește că funcția este monotonă pe linia reală întreg; specifica natura monotonie:

30.12 Determinați monotonia spațiilor funcționale:
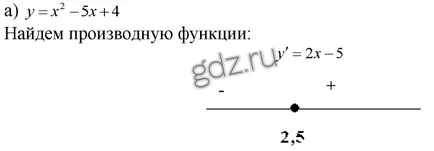

30.13 Determinați monotonia spațiilor funcționale:
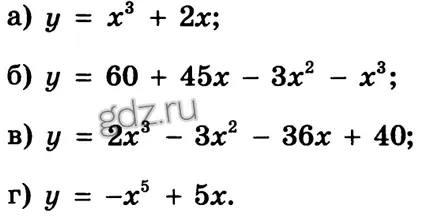



30,14 Exploreaza caracteristică pe monotonia:

30.15 Exploreaza caracteristică pe monotonia:


30.16 Exploreaza caracteristică pe monotonia:


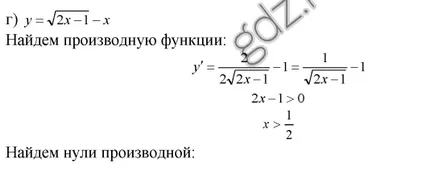

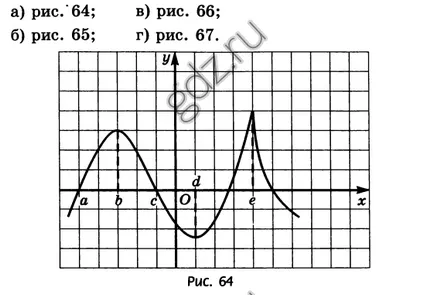
30,17 Conform graficului y = f (x), se arată într-o anumită figură, definește punctul în care derivatul său este egal cu 0:
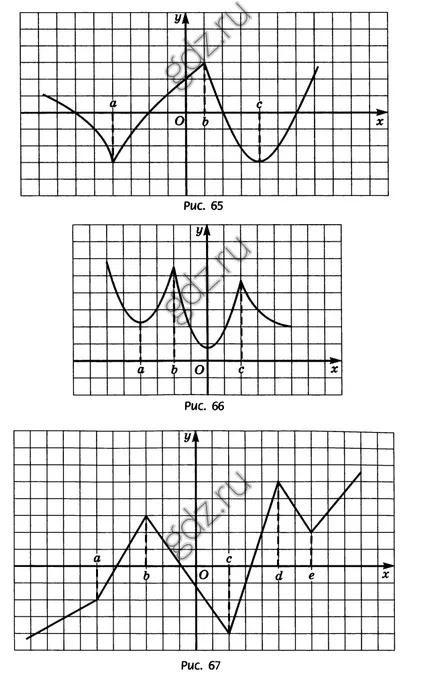
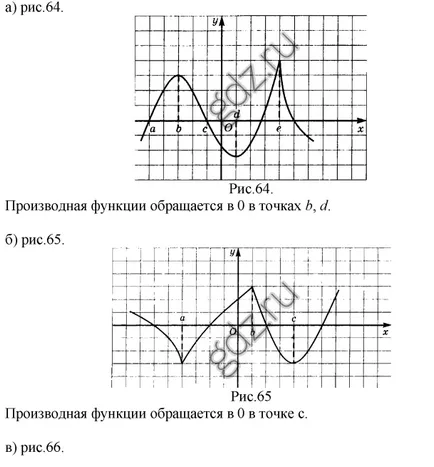
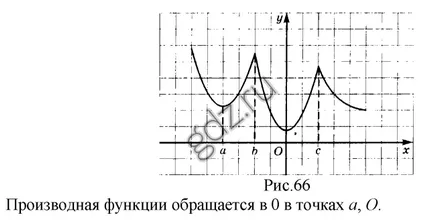
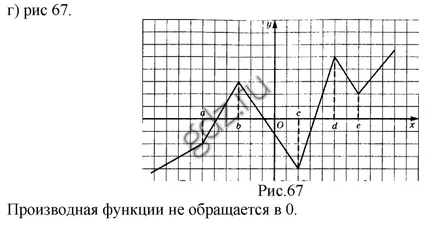
30.18 Conform graficului y = f (x), se arată în figură, definește punctul în care f „(x) nu există:

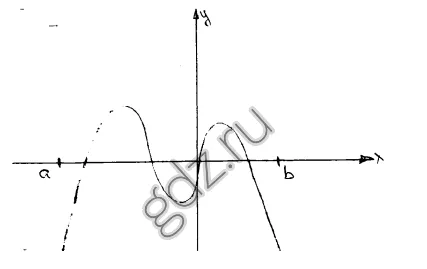
30,19 Cât de multe puncte minime are o funcție y = f (x), din care graficul este prezentat în figură:

30,20 Cât de multe puncte maxime este o funcție y = f (x), din care graficul este prezentat în figură:

30.21 Folosind datele din derivatul f „(x), prezentate în tabel indică:



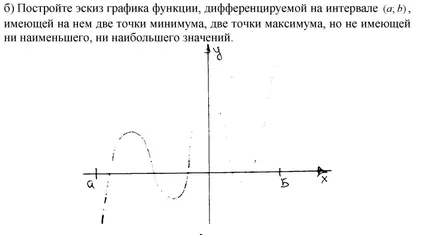
30.23 poate avea un singur punct de extremum:

30.24 În ce valori ale unei funcții date are un punct fix:

30,25 derivat Programat ilustrat în figura (222-223 cm ..), determină dacă funcția y = f (x) Puncte extremum:

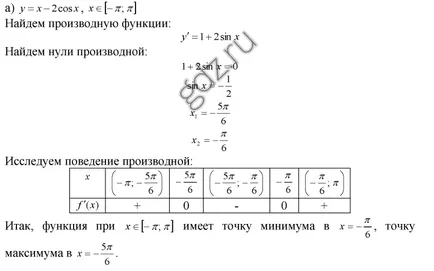
30.26 Găsiți punctele extremum ale unei funcții date, și să definească caracterul lor:


30.27 Găsiți punctele extremum ale unei funcții date, și să definească caracterul lor:

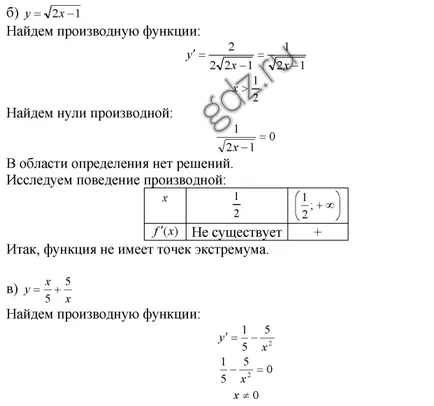

30.28 Găsiți punctele extremum ale unei funcții date, și să definească caracterul lor:
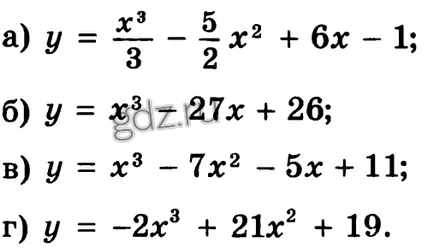

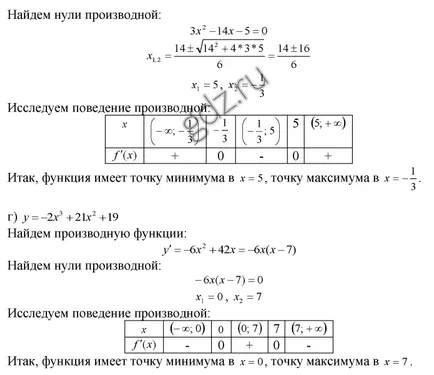
30.29 Găsiți punctele extremum ale unei funcții date, și să definească caracterul lor:
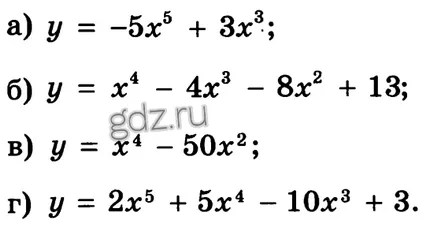


30.30 Găsiți punctele extremum ale unei funcții date, și să definească caracterul lor:
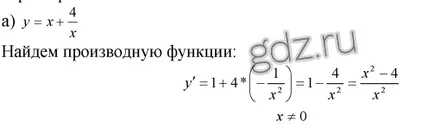

30.31 Găsiți punctele extremum ale unei funcții date, și să definească caracterul lor:


30.32 Găsiți punctele extremum ale unei funcții date, și să definească caracterul lor: