procese aleatoare ergodic - studopediya

proces aleatoriu staționar poate sau nu poate avea o proprietate ergodic. proprietate ergodicității este că orice realizare suficient de lungă a unui proces ergodic staționar este un fel de „reprezentant autorizat“ al întregului set de realizări ale procesului aleator și este posibil pentru a obține o idee a unui proces aleatoriu în ansamblul său.

Să ne explicăm acest lucru cu un exemplu dat caracteristici numerice - așteptări. Pentru o așteptare proces staționar - este constantă, și, prin urmare, poate fi estimat la orice secțiune transversală, având o mulțime de implementări. Pentru un proces ergodic staționar, același lucru se poate face cu o formă de implementare, dacă are o durată suficient de lungă. Aceasta este, pentru un proces ergodic staționar, valoarea medie a oricărei secțiuni transversale poate fi înlocuită cu valoarea medie a unei implementări suficient pe termen lung.

O condiție suficientă pentru a ergodicitate proces aleatoriu staționar este următoarea:

adică necesită ca odată cu creșterea secțiunilor de forfecare între funcția de corelare și atenuate în limita, atunci când t = ∞, zero.

Cu toate acestea, un proces aleatoriu staționar poate fi non-ergodic. Exemplele ergodice și procese aleatoare nonergodic prezentate în Fig. 6.5.

proces aleatoriu Nonergodicity poate fi cauzată, de exemplu, prin faptul că variabila aleatoare apare ca durata unui proces aleatoriu.

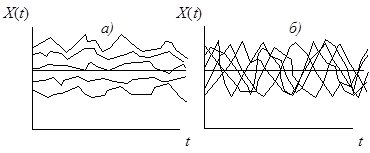
Figura 6.5. Implementările nonergodic (a) și ergodic (b) procese aleatoare staționare.

Să considerăm procesul aleator U (t):

unde X (t) - proces aleatoriu ergodic și v - o variabilă aleatoare medie și mv varianței și Dv.

Din teoria este cunoscut faptul că, în acest caz,

De aceea, această condiție nu este îndeplinită (6.29), și un proces aleatoriu U (t) este Nonergodic.

În practică, având doar o realizare a unui proces aleator (de exemplu, patruzeci și numărul de costurile medii anuale de apă), trebuie să acceptăm ipoteza staționaritate și ergodicitate. Deoarece numai în acest caz, estimarea caracteristicilor statistice obținute pentru această implementare, putem presupune toate caracteristicile unui proces aleatoriu.

Trebuie avut în vedere faptul că alegerea unui model probabilistic nu ar trebui să fie formală. Trebuie să fie ghidat de ambele considerații generale și date empirice pentru a modelului a fost consecvent și descrie în mod adecvat procesul în studiu.