Prezentarea „sarcina de a cântări“
prezentarea Related







Slide-uri și textul acestei prezentări

Sarcinile care urmează să fie cântărite
Finalizat: profesor de matematica MBOU Purekhovsky Scoala Suschikova Tatyana Alekseevna.

Dă-un om un pește - el va manca pentru o zi. Învață-un om de pește - el va manca pentru o viață întreagă. înțelepciunea chineză.

introducere
Matematica - una dintre cele mai vechi și mai importante științe. Mulți oameni au folosit cunoștințele matematice în vechi de mii de ani în urmă drevnosti-. Acestea sunt necesare pentru comercianți și constructori, topografi și soldați, preoți și călători. Și astăzi, nici o persoană nu se poate face în viață, fără o bună cunoaștere a matematicii. Această lucrare discută modalități de a rezolva aceste probleme, pentru a înțelege problema vechi, transmisă nouă din diferite țări și de ori, sarcina de a „monede falsificate“ sarcini pentru ajustarea folosind greutăți.

1. Obiectivele comparației folosind greutăți.
PROBLEMA 1. Pe de o greutate de pan 6 sunt mere și pere 3 sunt identice, pe de altă cupă identice - 3, cum ar fi mere și pere 5 din aceeași. Echilibrul este în echilibru. Ceea ce este mai ușor: un mar sau o para? SOLUȚIE: Deoarece echilibrul este în echilibru, și toate mere și pere toate identice în greutate, 6 mere pere + 3 = 3 + 5 mar pere; Scoateți cele două cupe de 3 mere si 3 pere, vom obține 3 mere = 2 pere, apoi 1 mar 1 para mai greu. RĂSPUNS: Pear mai greu.

1. Obiective pentru comparație utilizând greutățile.
2. OBIECTIVUL La o greutăți de cupă este o bucată de săpun, iar celelalte trei sferturi ale piesei și trei sferturi de kilogram. Echilibrul este în echilibru. Cât de greu este un bar de săpun? SOLUȚIE: împărțiți o bucată de săpun în 4 părți egale, apoi 4 părți egale săpun bar = 3 aceleași părți săpunului + 3/4 kg; Scoaterea din fiecare cupă la 3 părți, obținem: 1 parte = 3/4 kg, înseamnă o bucată de greutate de 3 kg. A: 3 kg.

2. Provocări pentru cântărirea în balanța cu greutăți.
SARCINĂ 3. Baron Munchausen 8 are 1g exterior identic Guirec în greutate, 2 g, 3G, ..., 8, își aduce aminte care unul dintre greutăți, cât de mult în greutate, dar numărul de Scleroză nu-l crede. Este Baron va fi capabil să dețină o ceașcă de cântărire în echilibru, în urma căruia va fi stabilită în mod clar în greutate de cel puțin una dintre greutățile? SOLUȚIE: Deoarece 7R + 8 g = g 1 + g 2 + g 3 + g 4 + 5d, 6d rămâne, prin urmare, într-o singură cântărire Baron poate stabili ponderi în greutatea unui 6 g otve. Da, el poate.

2. Provocări pentru cântărirea în balanța cu greutăți.
Digger SARCINĂ 4. Jack 9 kg minat de nisip. Va fi el capabil să măsoare trei cu o greutate de 2 kg de nisip folosind dvuhchashechnyh greutăți două greutăți - 200g și 50g? SOLUȚIE: Prima cântărire împărțirea nisipului în două grămezi la 4500 g, a doua - una dintre aceste grămezi pe două grămezi de 2250 g și, în final, de la unul dintre grămezi prin greutăți pavate 250 g Răspuns: poate.
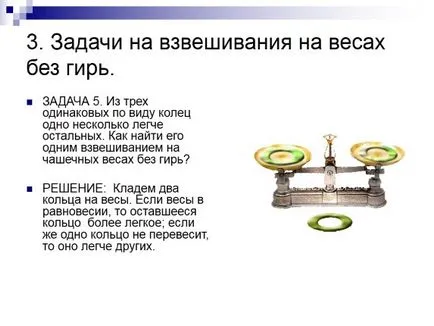
3. Provocări pentru cântărire pe cântar fără greutăți.
OBIECTIVUL 5. Dintre cele trei inele identice minte un pic mai ușor restul. Cum de a găsi o greutate de pe Bârnă? Soluție: Puneți două inele pe cântar. Dacă balanța este în echilibru, inelul rămas mai ușor; în cazul în care un inel nu este mai importantă decât mai ușor decât altele.

3. Provocări pentru cântărire pe cântar fără greutăți.
OBIECTIVUL 6. Dintre cele 101 identică în formă de monede, unul fals, caracterizate prin greutate. Cum se utilizează greutăți de cupă fără greutăți pentru o greutate de două pentru a determina restul mai ușor sau mai greu? Găsiți este necesar moneda contrafăcut. SOLUȚIE: Se cântăresc 50 de monede. Următoarele cazuri. 1) .Ravenstvo: Ia restul monedei și a pus-o în gramada stânga în loc de una dintre cele disponibile acolo. Apoi, dacă ai lăsat o grămadă de greu, monede falsificate este mai greu; și în cazul în care a lăsat o grămadă mai ușor, este mai ușor de monedă falsă. 2) .Neravenstvo: Luam o gramada mai greu și împărțiți-l în două grămezi de 25 de monede. Apoi, în cazul în care echilibrul este în echilibru, atunci moneda falsă este mai ușor în cazul în care greutatea grămezi inegale, atunci de monede falsificate este mai greu.

Concluzie.
Această lucrare este dedicată soluției de una din clasele de sarcini non-standard - Este sarcina cântăririi. Capacitatea de a rezolva astfel de probleme ajută la dezvoltarea gândirii logice, ingeniozitate, observație, spirit, care va ajuta în studiul de subiecte dificile în matematică în liceu.

Vă mulțumesc pentru atenție!