Prezentarea pe graficul y sin x - grafic undă sinusoidală de cos x y - cosinus
1

2 grafic al funcției y = sin x - sinusoidei
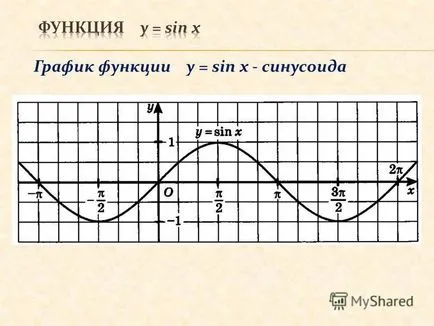
3 Graful y = cos x - cosinusoid
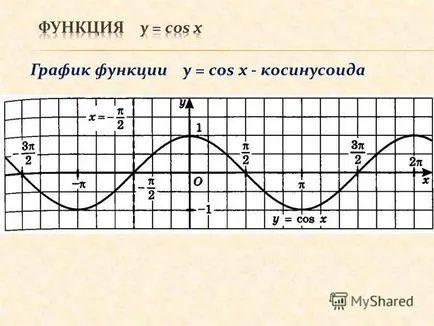
4 graph y = cos x - Proprietăți cosinus: 1.d (y) = (-; +) 2.E (y) = [- 1; 1] 3. T = 2π 4. y = cos x - chiar simetric funcția în raport cu graficul de ordonata 5. cos x = 0 pentru x = π / 2 + πn, n Z (zero) intervale de semn constant: cos x> 0 la - tt / 2 + 2πn la 0 - π / 2 + 2πn
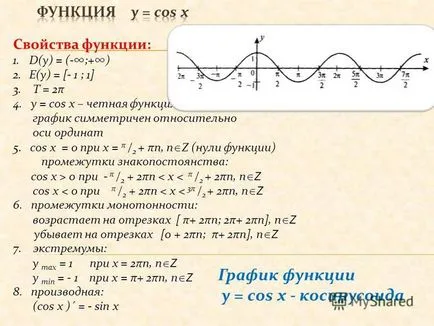
0 + 2πn la 0 0 pentru 0 5 + 2πn graficul y = sin x - Proprietăți ale funcției sinus: 1.d (y) = (-; +) 2. E (y) = [- 1; 1] 3. T = 2π 4. y = sin x - funcție ciudat, graficul este simetric față de origine 5. sin x = 0 pentru x = πn, n Z (zerouri) sin x> 0 pentru 0 0 + 2πn la 0 0 + 2πn la 0 + 2πn la 0 0 0 + 2πn la 0 + 2πn
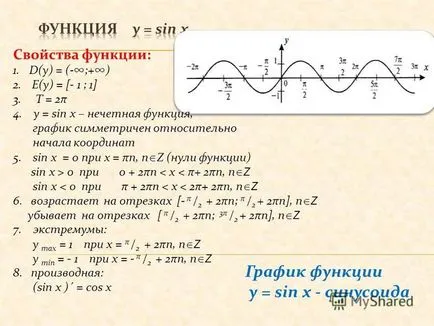
6

7 yx 1 π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 y = sin (x + π / 2) y = sin x = y funcție de construcții sin (x ± b) y = sin (x -π / 2)
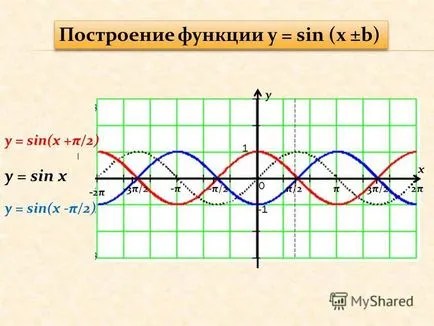
8, y = sin (x + / 4) Grafic funcție y = sin (x + / 4) Construirea funcției y = sin (x ± b)
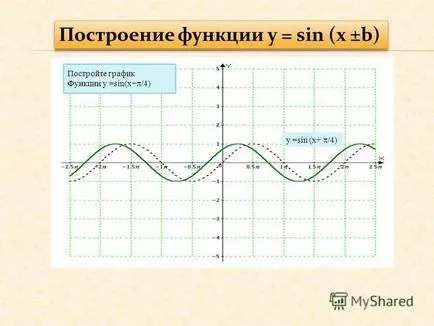
9 Funcția Grafic: y = sin (x - / 6) y = sin (x - / 6)
10 yx 1 π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 y = cos (x -π / 2) y = cos x = y Construcții Funcția cos (x ± π / 2) y = cos (x + π / 2)
11 1 y x π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 y = sin x 1 y = funcția sin x = y Construcții sin x ± b y = sin x -1
12 1 y x π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 y = cos x 1 y = cos x = y funcție de construcții cos x ± b y = cos x -1
13 Construcția funcției y = x MSIN
14 Construcția funcției y = MCOs x
15
16 Construcția funcției y = sin (k x)
17 Construcția funcției y = cos (k x)
18 Construcția funcției y = MCOs (k x)
Definiți o și 19 b, în cazul în care ASOS = x + b sau y = asin x + b. Definiți a și b, dacă ASOS = x + b sau y = asin x + b.
Definiți o și 20 b, în cazul în care ASOS = x + b sau y = asin x + b. Definiți a și b, dacă ASOS = x + b sau y = asin x + b.
Definiți o și 21 b, în cazul în care ASOS = x + b sau y = asin x + b. Definiți a și b, dacă ASOS = x + b sau y = asin x + b.
Definiți o și 22 b, în cazul în care ASOS = x + b sau y = asin x + b. Definiți a și b, dacă ASOS = x + b sau y = asin x + b.
Definiți o și 23 b, dacă ASOS = (x + b) sau y = asin (x + b). Definiți a și b, dacă ASOS = (x + b) sau y = asin (x + b).
Definiți o și 24 b, dacă ASOS = (x + b) sau y = asin (x + b). Definiți a și b, dacă ASOS = (x + b) sau y = asin (x + b).
Definiți o și 25 b, dacă ASOS = (x + b) sau y = asin (x + b). Definiți a și b, dacă ASOS = (x + b) sau y = asin (x + b).
Definiți o și 26 b, dacă ASOS = (x + b) sau y = asin (x + b). Definiți a și b, dacă ASOS = (x + b) sau y = asin (x + b).
0 pentru 0 "title =" Graficul y = tg x - Proprietăți tangensoida funcții: 1.D (y): 2. E (y) = 3. T = π 4. y = tg x - impar funcție simetrică graficul coordonatele 5. tg x = 0 pentru x = πn, n Z (zerouri) intervale de semn constant: tg x> 0 pentru 0 "class =" link_thumb „> 27 Graful y = tg x - proprietăți tangensoida funcții: 1.D ( y): 2. E (y) = 3. T = π 4. y = tg x - grafic impar simetrică funcție despre originea 5. tg x = 0 pentru x = πn, n Z (zerouri) intervale de semn constant: tg x> 0 pentru 0 0 + πn la 0 "> 0 + πn la 0 0 pentru 0" title = „Graficul y = tg x - proprietăți tangensoida funcții: 1.d (Y): 2. E (y) = 3. T = π 4. y = tg x - grafic impar simetrică funcție despre originea 5. tg x = 0 pentru x = πn, n Z (zerouri) intervale de semn constant: tg x> 0 pentru 0 "> 0 pentru 0" title = „Graficul y = tg x - proprietăți tangensoida funcții: 1.D (y): 2. E (y) = 3. T = π 4. y = tg x - grafic funcție ciudat simetrică originii 5. tg x = 0 pentru x = πn, n Z (zerouri) intervale de semn constant: tg x> 0 pentru 0 „>
28 graph y = ctg x - Proprietăți kotangensoida funcții: 1.D (ctg x). 2.E (ctg x) = 3. T = π 4. y = ctg x - grafic impar simetrică funcție despre originea 5. CTG x = 0 pentru x = tt / 2 + πn, n Z (zerouri) intervale de semn constant : c tg x> 0 pentru 0 0 + πn la 0 + πn
La 0 0 0 29 0 ca funcții Proprietăți: 1.D (arcsin x) = [-1; 1] 2.E (arcsin x) = 3. grafic funcție impar simetrică originii 4. y = 0 pentru x = 0 (zerouri) intervale de semn constant: y> 0 pentru la 0 0 0 0 0 0 pentru 0 pentru 0 la 0 0 pentru 0 pentru 0 0
La 0 -1 0 -1 la 30 Proprietăți funcție: 1.D (ARccOS x) = [-1; 1] 2.E (ARccOS x) = 3. Nu este par sau impar 4. y = 0 când x = 1 (zerouri) intervale de semn constant: y> 0 pentru la -1 0 -1 0 -1 la 0 pentru - 1 la 0 -1 0 -1 0 când la -1
0 pentru x> 0 y 0 pentru x> 0 y 31 Funcții Proprietăți: 1.D (arctg x) = 2.E (arctg x) = 3. grafic funcție impar simetrică originii 4. y = 0 pentru x = 1 (zerouri) intervale de semn constant: y> 0 pentru x> 0 y 0 pentru x> 0 y 0 pentru x> 0 y 0 pentru x> 0 y 0 pentru x> 0 y 0 pentru x> 0 y 0 pentru x> 0 y