Prezentarea pe algoritmizare ca o condiție necesară pentru automatizare - efectuat profesor

1 „ca o condiție prealabilă pentru automatizare algoritmică“ Finalizat știință profesor ASOSH 2: Sharipov II

2 Scop: 1) Scop: 1) și subiect material de fixare Repetiție: algoritm, proprietăți ale algoritmului, speciile de algoritmi de performanță și a graficelor de transformare; 2) Aplicarea cunoștințelor în domeniul matematicii.

3 Prin algoritm se înțelege clar și precis executor de instrucțiuni pentru a face o secvență de acțiuni care vizează realizarea obiectivului sau de a obține un rezultat specific. AP Ershov Proprietăți Algoritmul Algoritmul Tipuri de algoritmi

4 Tipuri de diagrame. diagrame de conversie.

6, o ecuație cerc în forma generală (x-x 0) 2 + (y-y 0) 2 = R2

0, pentru a obține graficul unei funcții y = f (x) + b trebuie graficul y = f (x) re "title =" transformări în raport cu axa OY. transfer paralel. Orarul de deplasare axa OY relativă este efectuată, dacă este necesar pentru a construi un grafic al unei y funcției = f (x) + b. Aici, în cazul în care b> 0, pentru a obține graficul funcției y = f (x) + b trebuie graficul y = f (x) re "class =" link_thumb „> 7 Conversie axe relativ OY. Transferențial paralelă. Graph în raport cu o schimbare axă OY, efectuată dacă este necesar să se construiască un grafic al unei y funcției = f (x) + b. în plus, în cazul în care b> 0, pentru a obține graficul funcției y = f (x) + b trebuie graficul y = f (x) să se deplaseze pe bedinits în pozitiv direcția OY axa (adică în sus), și în cazul în care b 0, pentru a obține graficul unei y funcției = f (x) + b trebuie graficul y = f (x) re „> 0, pentru a obține graficul y = f (x) + b trebuie graficul y = f (x) să se deplaseze în la bedinits ozhitelnom OY direcția axei (adică în sus), și dacă b "> 0, graficul pentru funcția y = f (x) + b trebuie y grafic = f (x) re" title = „transformări în raport cu axa OY. transferențial paralel. axa OY relativă program de deplasare se efectuează, dacă este necesar pentru a construi un grafic al unei y funcției = f (x) + b. În plus, în cazul în care b> 0, pentru a obține graficul funcției y = f (x) + b trebuie y grafic = f (x) re „>

0, atunci graficul funcției y = f (x) trebuie să fie deplasat în axa negativă direcția OX (în „title =“ Transformările în raport cu axa OX. Transferențial paralelă. Transferul paralel (offset) generat axa relativă OX se realizează pentru trasarea y = f (x + a). Dacă a> 0, atunci graficul funcției y = f (x) trebuie să fie deplasat în axa negativ direcția OX (a "class =" link_thumb „> 8 Conversion relativ axa OX. transferențial paralelă. transferul paralel (offset) generat relativ axa OX este realizată pentru trasarea y = f (x + a). Dacă a> 0, atunci graficul funcției y = f (x) trebuie să fie deplasat de pe Axa direcția OX itsatelnom (stânga) de către o unitate. Dacă 0, atunci graficul funcției y = f (x) trebuie să fie deplasat în axa negativă direcția OX (a „> 0, atunci graficul funcției y = f (x) trebuie să fie deplasate în sens negativ axa direcție OX (stânga) de către o unitate. Dacă „> 0, graficul funcției y = f (x) trebuie să fie deplasat în axa negativă direcția OX (în“ title = „transformările în raport cu axa OX. transferențial paralel. transferul paralel (schimbare ) generate în raport cu axa OX funcționează la y parcelei = f (x + a). Dacă a> 0, atunci graficul funcției y = f (x) trebuie să fie deplasat în axa negativă direcția OX (a „> 0, atunci graficul funcției y = f (x) trebuie să fie deplasat în axa negativă direcția OX (în«title =»Conversion axa relativ OX. transferențial paralelă. transferul paralel (offset) generat axa relativă OX se realizează pentru trasarea y = f (x + a). Dacă a> 0, atunci graficul funcției y = f (x) trebuie să fie deplasat în axa OX direcție negativă (în „>

9 Procesul de ramificare legat la graficele de transformare prezintă problema Luați în considerare: Este necesar să se creeze un algoritm care calculează valoarea introdusă a funcției valorii argument dat într-un grafic în intervalul [-3, 3].

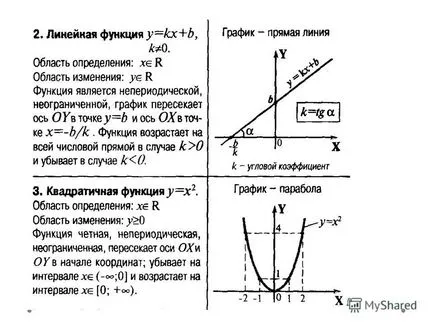
10 pe intervalul [-3; -2) vedem o linie dreaptă care trece prin punctele cu coordonate (-3, 1) și (-2: 1). Ecuația liniei în formă generală y = kx + b. Pentru a determina ecuația dreptei este necesară pentru a substitui valorile lui x și y în ecuația generală a liniei și a creat un sistem. De la I II I II ecuația de scădere și de a obține ecuația 2 = -k, deci k = -2 k Acum substituim în ecuația I. 1 = (-2) * (- 3) + b Din această ecuație găsim b. b = -5 Acum substituind valorile obținute k și b în ecuația generală a unei linii drepte, obținem funcția dorită y = -2x-5. Pentru a începe soluția chiar cea mai simplă problemă aveți nevoie de o descriere clară a intrărilor și ieșirilor sale. Găsim domeniu al acestei funcții este: [-3, 3].

11 Dacă argumentul x în intervalul [-2; 0), atunci raza semicercului este 1, ectopic pe axa OX de origine la stânga și în jos pe axa OY de 1 unitate. Acest cerc este definit de ecuația: (x + 1) 2 + (y + 1) 2 = 1. exprimă Așadar y: y = ± 1, dar pentru că avem nevoie doar semicercul de jos, atunci y = Să considerăm acum intervalul [0; 1). Grafic este o linie dreaptă: y = x-1. Dacă argumentul x aparține intervalului [1; 3] este un grafic al semicercului superioare a razei 1, originea ectopic pe axa OX la dreapta cu 2 unități. Un astfel de grafic este descrisă de ecuația: = y. Astfel, obținem următoarea funcție: Y =

12 de intrare x (x 3) Valoarea trebuie să aparțină intervalul [-3, 3] Output Da Nu X

13 lucrari frontale necesare pentru a crea un algoritm care calculează valoarea introdusă a valorii funcției argument. 1. La ce interval este necesar să se calculeze valoarea funcției? 2. Cum vedeți funcția pe intervalul [-9; - 6)? 3. Este necesar să-și exprime y. 4. Introduceți funcția dorită în intervalul [-6; 3)? Funcția 5.Zadayte pe intervalul [-3, 0)? Interval 6.Rassmotrim [0; 3). 7.Funktsiya în intervalul [3; 9]. Y =