Prezentare - un sistem de ecuații liniare cu trei variabile

O scurtă descriere a documentului:

Prezentarea „sistem de ecuații liniare cu trei necunoscute“ este destinat utilizării în clasa de matematică în clasa a 7-a și pentru educație extrașcolară. Aceasta ajută la crearea unei abilitate de clasa a saptea in rezolvarea unui sistem de ecuații metoda de substituție liniară. Această metodă este cea mai ușoară, printre altele, ușor de învățat elevii. El a stăpânit de clasa a saptea pentru a rezolva sisteme de ecuații liniare cu două variabile. Dar eficiența procesului pentru a rezolva probleme mai complexe, care nu le-au testat încă în practică. Ei trebuie să se asigure că creșterea numărului de necunoscute nu neagă eficacitatea acestei metode. Ca urmare a setului standard de operațiuni care sunt valabile pentru orice număr de variabile și numărul corespunzător de ecuații, elevul poate să se asigure că această metodă poate fi aplicată în alte cazuri în care o decizie trebuie să găsească valoarea variabilelor sistemului.

Animation utilizate în prezentare, demonstrează structurile de alocare a parsat, transformarea lor, substituirea expresiilor transformate. Această animație care însoțește linia de raționament în rezolvarea unor astfel de probleme, care să permită studenților să formeze o idee clară a modului de substituire și utilizarea acesteia în practică, amintiți-vă cursul soluției.

Această prezentare ar trebui să fie utilizată pentru a consolida abilitățile de sisteme de ecuații liniare metoda de substituție de rezolvare, precum și pentru introducerea conceptului unui sistem de ecuații liniare cu trei variabile și moduri de a le rezolva.

diapozitive 1-2 (Tema prezentării „Sistemul de ecuații liniare cu trei variabile“, un exemplu)

Prezentarea începe cu o introducere la conceptul de ecuații liniare cu trei variabile. Ecranul afișează o înregistrare a structurii algebrice matematice. Se afișează apoi numele pe care doriți să vă amintiți. Următoarele subliniază faptul că fiecare variabilă este singura. Din ecuații liniare de acest tip pe următoarele componente glisante ale sistemului. Fiecare ecuație conține trei variabile litere coeficienți și membri liberi conțin un index, care arată că acesta aparține unei anumite ecuații. Astfel, studentul demonstrează o prezentare generală a unui sistem de ecuații liniare cu trei necunoscute.

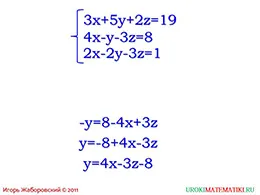
Sistemele Soluții Explicatie cu trei variabile include, de exemplu, care cuprinde un sistem de ecuații, în care fiecare coeficient nu este 0, astfel încât să nu pentru a distrage cazuri speciale atenția elevilor în timpul soluțiilor procesului de dezvoltare. Observați că coeficientul variabila y în a doua ecuație este -1, ceea ce facilitează eliminarea formulei pentru găsirea variabila ecuației. Pentru claritate, ecuația este scos din sistem și demonstrează transformarea acestuia cu transferul membrilor rămași ai dreptului egalitate. Apoi, prin înmulțirea egal totală -1 și termeni pentru comoditate rearanjarea, o formulă este obținută pentru construirea de substituție în celelalte ecuații în înlocuirea. Ecuațiile de transformare Identic au stăpânit de clasa a saptea, asa ca folosesc doar o abilitate în a face cu sarcini similare. De fapt, astfel de argumente pot fi făcute în minte, astfel încât cu ajutorul animației arată dispariția modificărilor de curs, lăsând formula pentru înlocuirea și apoi includerea acestuia în sistemul de ecuații.

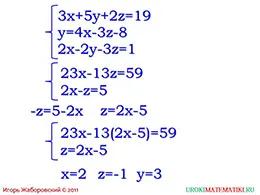
Următorul pas al glisierei prezintă o expresie de substituție obținută în a doua ecuație. Ca rezultat al acestei substituției, obținem un sistem de două ecuații, soluția din care elevii de clasa a șaptea au însușit deja. După console de expansiune și reducând termeni similari elevi ușor de ghicit construcții familiare. Întregul curs de transformare, care a dus la acest design este îndepărtat din soluție, pentru a arăta elevilor modul în care sistemul de trei ecuații cu trei variabile transformate într-un sistem de două ecuații cu două variabile. Apoi, într-una din ecuațiile z este pe partea stângă, precum și celelalte condiții de egalitate, folosind regulile de transfer se depun la dreapta. După multiplicarea prin egalitate -1, obținem o ecuație care definește o expresie pentru substituirea a doua ecuație în loc de z. Apoi, pasul următor este demonstrată prin substituirea expresiei rezultată pentru z în prima ecuație. Se pare ecuație liniară convențională cu o singură variabilă x, care poate fi ușor de stocat. Astfel, am ajuns la găsirea de soluții ale sistemului. Substituind valoarea obținută a x în expresia pentru căutarea la z, iar apoi cele două soluții - expresia pentru căutarea în, găsi soluția unică de ecuații cu trei variabile.

Descrierea detaliată a procesului de substituție în această prezentare este importantă pentru o înțelegere aprofundată a mecanismului de aplicare a acestei metode. Prezentare „Sistemul de ecuații liniare cu trei necunoscute“ pot fi folosite pentru a genera soluții de calificare în acest mod în lecția, precum și pentru elev muncă independentă și de învățare la distanță.